
UNIVERSITY EXAMINATIONS: 2017/2018
EXAMINATION FOR THE DIPLOMA IN INFORMATION
TECHNOLOGY
DIT401 PROBABILITY AND STATISTICS
FULLTIME/PARTTIME
DATE: APRIL, 2018 TIME: 1 ½ HOURS
INSTRUCTIONS: Answer any THREE questions.
QUESTION ONE
a) The probability that an entering college student will graduate is 0.4. Determine the
probability that out of 5 students
i. None will graduate (3 Marks)
ii. One students will graduate (3 Marks)
iii. At least one will graduate (3 Marks)
iv. All students will graduate (3 Marks)
b) The following is data on the heights of seedlings in a certain tree nursery
3.1 5.1 3.7 4.1 6.8 5.0 3.2 6.0 5.3 4.5 6.4 5.4
5.3 8.3 5.2 5.5 7.3 6.5 6.6 7.5 5.7 5.9 4.8 7.0
7.1 4.0 6.3 4.7 4.8 3.6
Prepare a grouped frequency distribution and find the mean of the
grouped data (8 Marks)
QUESTION TWO
a) Find the correlation coefficient by karl pearson’s method between x and y and
interpret its value
X 57 42 40 33 42 45 42 44 40 56 44 43
Y 10 60 30 41 29 27 27 19 18 19 31 29
(4 Marks)
b) Births in a hospital occur randomly at an average rate of 1.8 births per hour. What is
the probability of observing 4 births in a given hour at the hospital? (4 Marks)
c) The table below gives the probability distribution of a discrete random variable x.
Given that p(x<13) = 0.75, find the value of k and q hence calculate E(x) (4 Marks)

d) The probability that i hit a target is 1
4
, and the probability that b hits the target is 2
5
.
Both shoot at the target. Find the probability that
(i) At least one of them hits the target. (3 Marks)
(ii) Neither hits the target (2 Marks)
e) The probability that a student owns a computer is 0.65 and the probability that a
student owns a phone is 0.82. If the probability that a student owns both is 0.55. What
is the probability that a given student owns either a phone or a computer (3 Marks)
QUESTION THREE
a) The weight of 8 diploma students were taken in variable x as they reported and the
following results calculated.
![]()
i. Calculate the mean and the standard deviation of x (3 Marks)
ii. The mean and standard deviation of x after two more students weighing 58kg
and 60 kg respectively join the group (3 Marks)
iii. The mean and the standard deviation of x after each of the 8 students had lost
2kg. (3 Marks)
b) A class has 10 boys and 5 girls, three students are selected at random. Using tree
diagram find the probability that.
(i) All are girls (3 Marks)
(ii) First 2 are boys (3 Marks)
(iii)First and third are of the same sex and the second of opposite sex(5 Marks)
X 4 8 12 15 20
P(x) k 0.25 0.3 q 0.1
QUESTION FOUR
a) In a study of the daily production of a company over 50 days, the following data was
corrected
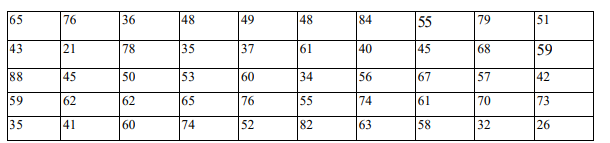
i. Starting with a class 20-29, group this data into a frequency distribution. (5 Marks)
ii. using a suitable assumed mean, calculate the mean and standard
deviation of this data. (6 Marks)
b) in a bag of 40 vegetables, 25 are carrots and 15 are potatoes. The mean weight of the
carrots is 60grams while that of the potatoes is 52 grams. The standard deviations of the
weights are 4 grams and 6 grams for the carrots and potatoes, respectively. Calculate the
mean and standard deviation of all the vegetables in the bag. (6 Marks)
c) In a large flower farm, 20% of a particular kind of flower is red, while all the rest are
white. The farmer decided to take a sample of three flowers from his farm. The third
flower that he picked was white. By use of a tree diagram, find the probability that the
first two flowers he picked were red, given that the third flower is white. Assume
picking with replacement. (3 Marks)
QUESTION FIVE
a) Differentiate between the following terms as used in statistics
i. Qualitative and quantitative variables (2 Marks)
ii. Population and sample (2 Marks)
iii. Discrete and continuous variables (2 Marks)
b) The numbers of points scored in each game by a college team were recorded as
follows.
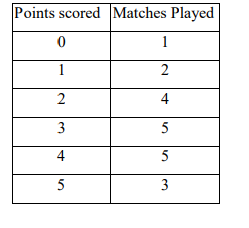
Calculate
i. Mean (3 Marks)
ii. Variance (3 Marks)
iii. Standard deviation (3Marks)
c) A certain data set was collected on a random variable x and the following summaries
made:
![]()
i. Find the mean and the standard deviation (3 Marks)
ii. Write down the answers to (i) if ‘10’ is subtracted from each of the
original values
