 UNIVERSITY EXAMINATIONS: 2015/2016
UNIVERSITY EXAMINATIONS: 2015/2016
EXAMINATION FOR THE DIPLOMA IN BUSINESS/ INFORMATION
TECHNOLOGY
DIT 401 PROBABILITY AND STATISTICS
DATE: AUGUST 2016 TIME: 1½HOURS
INSTRUCTIONS: Answer Any THREE Questions.
QUESTION ONE
a) Distinguish between
i) Discrete and continuous data. (2 Marks)
ii) Qualitative and quantitative variables (2 Marks)
iii) Multivariate and bivariate data (2 Marks)
b) i) Organize the data below into a grouped frequency distribution.
2370 1970 1540 1830 1500 2300 1750 1570
1740 1860 1290 2030 2370 2140 1830 1030
2610 1570 2400 1780 3220 2320 920 1650
3080 2960 2460 1250 2160 2520 2860 2700
1580. (8 Marks)
ii) From distribution obtained in b (i) above, calculate:-
i. The mean (2 Marks)
ii. The mode (2 Marks)
iii. The standard deviation (2 Marks)
QUESTION TWO
(a) Distinguish between
i) Linear regression and Linear correlation (3 Marks)
ii) Skewed and normally distributed data (3 Marks)
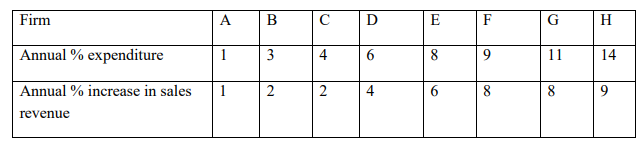
(b) Use least squares regression line to estimate the increase in sales revenue expected from an
increase of 75% in advertising expenditure (14 Marks)
QUESTION THREE
a) Given the data set:
43, 75, 48, 51, 47, 50, 20, 37, 55, 93, 75, 78, 16, 34, 86, 73, 55, 86, 72, 73, 48.
i) Find Q1 and Q3 (2 Marks)
ii) Find median (2 Marks)
iii) The interquartile range (IQR) and the semi interquartile range (SIQR). (3 Marks)
c) A sample of 250 students was used to indicate their favorite TV station.
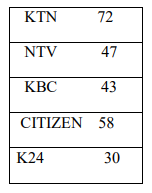
Represent this data in a pie chart. (4 Marks)
c) Define, with the help of a Venn diagrams the following
i) Intersection of two sets, A & B (3 Marks)
ii) Union of three sets A, B, and C (3 Marks)
iii) Disjoint sets X, Y, and T (3 Marks)
QUESTION FOUR
a) A deck of 52 cards has 13 spades. If 2 cards are drawn at random,
determine the probability that both cards are spades. (4 Marks)
b) A class has 10 boys and 5 girls. 3 students are picked at random.
i) Represent this information on a tree diagram (4 Marks)
and determine the probability that
ii) All are girls (2 Marks)
iii) The first two picked students are boys. (2 Marks)
iv) The 1st and 3rd are of the same sex and the 2nd of the
opposite sex (2 Marks)
c) A coin is tossed 3 times. Use the binomial formula to determine the probability
of getting exactly 2 heads (3 Marks)
d) If the coin is tossed 10 times, determine the probability of observing exactly 8
heads. (3 Marks)
QUESTION FIVE
a) Give brief explanations of the following statistical distributions.
i) Normal distribution (2 Marks)
ii) Poisson distribution (2 Marks)
iii) Exponential distribution (2 Marks)
b) Customers arrived randomly at a department store at an average rate of
3.4 persons per minute. Assuming that the customers arrive, calculate the probability
that:
i) No customer arrives at any particular minute. (3 Marks)
ii) Exactly are customer arrive in any particular minute (3 Marks)
iii) One or more customers arrive in 30 seconds. (3 Marks)
c) The table below gives the probability distribution of a discrete random variable of
X<13 = 0.75. Find the values of k and q and hence calculate E(x) (5 Marks)
x 4 8 12 15 20
P(x) k 0.25 0.3 q 0.1
