
UNIVERSITY EXAMINATIONS: 2018/2019
EXAMINATION FOR THE DIPLOMA IN BUSINESS INFORMATION
TECHNOLOGY
DBIT 103: FOUNDATION OF MATHEMATICS
DATE: AUGUST 2019 TIME: 2 HOURS
INSTRUCTIONS: Answer QUESTION ONE and any other TWO Questions.
QUESTION ONE
a) In a class of 100 students, 40 take Agriculture, 63 take Biology while x students take both the two
subjects. If 12 students take neither Biology nor Agriculture, find:
i) x (4 Marks)
ii) The number of students that take just one of the two subjects (4 Marks)
b) A Tautology is a formula which is always True for every value of its propositional variables.
Prove [(p →q) ∧ p] → q is a tautology (5 Marks)
c) Find the inverse of the following function f(x) = x − 3 (3 Marks)
d) Define each of the following sets using both the Roster and the Set Builder methods
i) N − the set of all natural numbers (3 Marks)
ii) Z − the set of all integers (3 Marks)
e) Find the domains and ranges of each the following functions
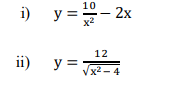
QUESTION TWO
a) Consider the functions
?(?) = ? + 2 and
?(?) = 2? + 1, Find a formula for the composition functions:
2
2
i) (f g) (x) (4 Mark)
ii) (g f) (x). (4 Mark)
b) Define the following terms
i) One-to-one (or injective ) Functions (4 Marks)
ii) Onto (or surjective) Functions (4 Marks)
iii) One-to-one correspondence (or bijective) Functions (4 Marks)
QUESTION THREE
a) Distinguish between a function and a relation (3 Marks)
b) Let A=
a,b,c,d,e
and B be the set of letters in the alphabet. Let the functions ?, ? and ℎ
from A into B be defined as follows:
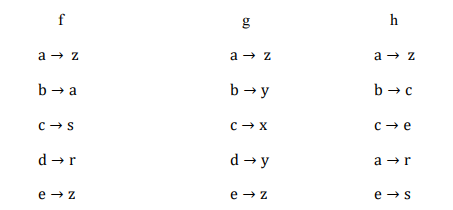
c) State, with reasons, which among the three is (are) a function(s) and which is (are)
a relation(s) (3 Marks)
d) Define the following terms giving examples of how each is represented
i) Real numbers
ii) Irrational numbers
iii) Null set (6 Marks)
e) A survey of 60 students showed that 30 played football, 19 played Rugby and 25 played Basketball.
Further analysis showed that 11 played both Basketball and Rugby, 10 played both Football and
Rugby whereas 12 played both Basketball and Football. 8 of the students played all the three games.
i) Represent the above information on a Venn diagram and (2 Marks)
ii) Hence or otherwise determine the number of students surveyed that:
• Played none of the three games. (2 Marks)
• Played a maximum of two games. (2 Marks)
QUESTION FOUR
a) Define, with the help of truth tables and using propositional variables p and q, the following
connectives:
i) Negation (2 Marks)
ii) Conjunction (2 Marks)
iii) Disjunction (2 Marks)
iv) Implication (2 Marks)
b) A Contradiction is a formula which is always False for every value of its propositional variables.
Prove ( p ∨ q) ∧ [( ̴p) ∧ ( ̴q ) ] is a contradiction (6 Marks)
c) A Contingency is a formula which has both some True and some False values for every value
of its propositional variables. Prove (p ∨ q) ∧ ( ̴q) it is a contingency (6 Marks)
QUESTION FIVE
a) Played just one game. (2 Marks)
b) Define each of the following terms as used in set theory
i) Universal Set
ii) Empty (Null) Set
iii) Singleton Set
iv) Equivalent Sets (8 Marks)
c) Find the inverse of the following function: f(x) =
1
x +1
d) List the elements of the following sets
i) A = {x: x ∈ N, 3 < ? < 9} (2 Marks)
ii) B = {x: x ∈ N, x
2 + 1 = 10} (2 Marks)
iii) C = {x: x ∈ N, x is odd , −5 < ? < 5} ` (2 Marks)
e) Draw a Venn diagram of sets A, B, C where A ⊆ B, sets A and C are disjoint
but B and C have elements in common
