TUESDAY: 25 April 2023. Morning Paper. Time Allowed: 3 hours.
Answer ALL questions. Marks allocated to each question are shown at the end of the question. Show ALL your workings. Do NOT write anything on this paper.
QUESTION ONE
1. Highlight FOUR characteristics of a good questionnaire as a tool for collecting primary data (4 marks)
2. In relation to research, explain the following terms:
- Non-probability (2 marks)
- Population (2 marks)
- Sampling frame (2 marks)
3. A research study of 200 households was carried out on the preferred beverages for breakfast among tea, coffee or The research yielded the following information:
70 households preferred Tea
72 households preferred Coffee
65 households preferred Cocoa
30 households preferred both Tea and Coffee
20 households preferred both Tea and Cocoa
35 households preferred both Coffee and Cocoa
10 households preferred all the three beverages
Required:
- Present the above information in form of a Venn diagram (4 marks)
- Determine the number of households who preferred only one beverage (2 marks)
- Determine the number of households who preferred more than one beverage (2 marks)
- Calculate the number of households that preferred at least one beverage (2 marks)
(Total: 20 marks)
QUESTION TWO
1. The 10th term in an arithmetic progression (AP) series is 29 and the 14th term is 45
Required:
- The first term and common difference in the (3 marks)
- The sum of the terms between the 40th term and the 80th term boundaries (3 marks)
2. A trader left Kenya for Britain with 1,580,000. The plane made an emergency landing in South Africa where he stayed for 4 days.
The trader converted all his monies to South African Rands. He spent 1,800 South African Rands per day on food, 1,150 Rands per day on accommodation and 2,250 Rands on souvenirs.
Upon reaching Britain, he converted all his monies to UK Pounds (£) where he paid for machinery at US dollars
$5,200 plus a 5% charge on duty and freight.
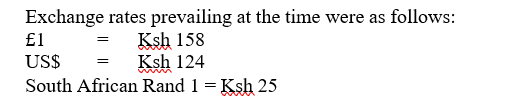
Required:
- The amount of money in South African Rands remaining with the trader when leaving South (3 marks)
- The amount of money the trader had in Kenya shillings (Ksh) after paying for the (4 marks)
3. Silas Mbaya deposited Sh.350,000 in a bank account for several years. The money earned interest at a rate of 18% per annum compounded quarterly. Silas intends to purchase a piece of land at a cost of 720,000.
Required:
- Calculate the number of years it would take Silas Mbaya to purchase the piece of (3 marks)
- Silas Mbaya has decided to add 200,000 into the account after one year.
Calculate the number of years that Silas Mbaya would reduce the waiting time calculated in (c) (i) above in order to buy the piece of land. (4 marks)
(Total: 20 marks)
QUESTION THREE
1. Outline THREE advantages of piece rate method of labour (3 marks)
2. Evaluate the following integrals:

3. The data below shows the quantity of maize flour produced by a maize miller over a period of six months in thousands of bags:
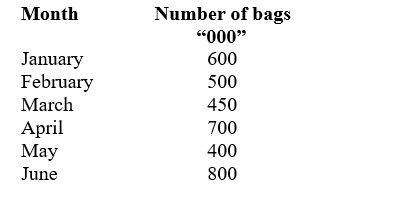
Required:
Using January as the base month, calculate the quantity index using the following methods:
- Fixed base (3 marks)
- Chain base (3 marks)
4. The research department of XYZ Ltd. has 5 male employees and 7 female employees. The head of department wishes to form a research team of five employees.
Required:
Determine in how many ways the research team could be formed such that it has 3 male and 2 female employees. (5 marks)
(Total: 20 marks)
QUESTION FOUR
1. Using an illustration in each case, differentiate between “mutually exclusive events” and “dependent events” as used in probability (6 marks)
2. An employee’s probability of waking up on time is ⅔. If she wakes up on time, there is a probability of 9/10 that she will catch the train and be on time for work. If she misses the train, there is a probability of ¼ that she will be on time for work
Required:
- Draw a tree diagram to represent the above (3 marks)
- The probability that the employee catches the (2 marks)
- The probability that the employee is late for work. (2 marks)
- The probability that the employee oversleeps and she is on time for work. (2 marks)
3. The sales revenue of 20 thermos flasks and 12 cups is Sh.39,600. The sales revenue for 8 thermos flasks and 17 cups is 19,500. The selling price of each of the item had a mark up of 20%.
Required:
- The selling price of each of the items using matrix (3 marks)
- The cost price per (2 marks)
(Total: 20 marks)
QUESTION FIVE
1. Citing an example in each case, explain THREE types of mathematical equations whose degree of polynomial is greater than zero and less than (6 marks)
2. The following raw data shows marks scored by 40 students in a statistics test:

Required:
- Present the above data in a grouped frequency distribution table starting from the class of 50 – (5 marks)
- Present the results in (b) (i) above in an ogive curve (5 marks)
- Using the ogive curve in (b) (ii) above, estimate the value of quartile deviation (3 marks)
- State the modal class (1 mark)
