
UNIVERSITY EXAMINATIONS: 2018/2019
EXAMINATION FOR THE DEGREE OF BACHELOR OF SCIENCE IN
INFORMATION TECHNOLOGY / BACHELOR OF BUSINESS
INFORMATION TECHNOLOGY/ BACHELOR OF SCINCE IN APPLIED
COMPUTING
BIT 2201/BIT 308/BAC 2106: SIMULSTION AND MODELING
FULL TIME/PART TIME/DISTANCE LEARNING
DATE: APRIL, 2019 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions.
QUESTION ONE [30 MARKS]
a) Define the term simulation? [2 Marks]
b) Explain the role of computers in simulation. [3 Marks]
c) State four short comings of the mid-square method as generator of random numbers.
[4 Marks]
d) Using appropriate examples distinguish between discrete event simulation and
continuous event simulation. [4 Marks]
e) Using a mixed congruential method to generate a sequence of five two-digit random
integer number such that
![]()
. [5 marks]
f) What is autocorrelation? How does it does it affect simulation analysis? [5 Marks]
g) With the help of a single queueing model having inter-arrival and service time constants
1.4
and
minutes respectively and taking
10
minutes as the simulation period .
Assume that initially the system is empty and the first customer arrives at time
t 0.
Determine the:
i. Average waiting time of a customer. [3 Marks]
ii. Average waiting time per customer for those who must wait.
[3 Marks]
iii. Percentage idle time of the facility. [1 Mark]
QUESTION TWO [20 MARKS]
a) Not simulation and modeling exercises are a success. Discuss five common pitfalls to
successful simulation. [5 Marks]
b) According to the test, a Poisson deviate with parameter
can be generated by
finding the number of exponential random deviates used to satisfy the following
inequality.
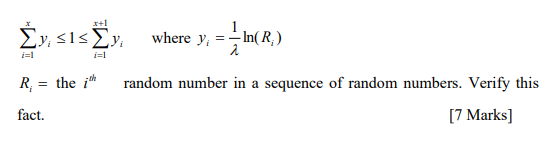
the
th i random number in a sequence of random numbers. Verify this
fact. [7 Marks]
c) With the help of labeled diagrams illustrate and describe the four types of queues
that exists giving common place examples. [8 Marks]
QUESTION THREE [20 MARKS]
a) State four properties of a good random number generator. [4 Marks]
b) Define the terms verification and validation in the context of modeling.
[4 Marks]
c) A dentist schedules all his patients for
30 -minute appointments. Some of the patients
take more than
30
minutes, some less, depending on the type of dental work to be done.
The following summary shows that various categories of work, their probabilities and
time actually needed to complete the work.
Category of service Time required (minutes) Probability of category

Simulate the dentist’s clinic for four hours and determine the average waiting time for
the patients as well as the idleness of the doctor. Assume that all patients show up at the
clinic at exactly their scheduled time starting at 8:00 a.m. Use the following random
numbers for handling the above problem:
40, 82, 11, 34, 25, 66, 17, 79
[12 Marks]
QUESTION FOUR [20 MARKS]
a) Describe the three factors that should be considered when selecting a simulation
language. [6 Marks]
b) Discuss the Monte Carlo simulation method of solving problem, illustrating it by
outlining a procedure to solve a specified problem of your choice. [8 Marks]
c) Distinguish between solutions derived from simulation models and solutions derived
from analytical models? [6 Marks]
QUESTION FIVE [20 MARKS]
a) Explain the three factors to consider when designing a simulation experiment.
[6 Marks]
b) A confectioner sells confectionary items. Past data of demand per week (in hundred
grams) with frequency is given below:
Demand/week
![]()
Using the following sequence of random numbers
35, 52, 90,13, 23, 73, 34, 57, 35,83, 94, 56, 67, 66, 60
generate the demand for the next
15
weeks .
(i) Using the formula determine the expected demand per week. [3 Marks]
(ii) Determine the average demand per week using the simulated data. [3 Marks]
(iii)Comment on the results in (i) and (ii). [2 Marks]
c) Simulation models are not the only models that can be used for understanding and
improving the real world. There exist other modeling approaches. Why would
simulation be used in preference to these other modeling approaches.
[6 Marks]
END
