
UNIVERSITY EXAMINATIONS: 2016/2017
ORDINARY EXAMINATION FOR THE DEGREES OF BACHELOR OF
SCIENCE IN INFORMATION TECHNOLOGY/ BACHELOR OF
BUSINESS IN INFORMATION TECHNOLOGY
BIT2201 BBIT308 SIMULATION AND MODELING
FULLTIME/PART TIME/DISTANCE LEARNING
DATE: AUGUST, 2017 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions.
QUESTION ONE: 30 MARKS (COMPULSORY)
a) Discuss the two short comings of the mid-square method as generator of random numbers.
(4 Marks)
b) Using the Linear Congruential Generator (LCG) with a=67, m=31, c=17 and seed Z0 = 117
generate the first FIVE random variates on [0,1]. (6 Marks)
c) Using appropriate examples identify four main types of system. (4 Marks)
d) Explain what initialization of the simulation model entails. (2 Marks)
e) Simulation models are not the only models that can be used for understanding and improving
the real world. There exist other modeling approaches. Why would simulation be used in
preference to these other modeling approaches? (6 Marks)
f) With the help of well labeled diagrams illustrate and describe the four types of queues that
exist giving common place examples. (8 Marks)
QUESTION TWO: 20 MARKS
a) Describe five common statistics included in the output report of a simulation programming
system. ` (5 Marks)
b) Discuss the time adjustment mechanisms used in discrete-event simulation models
highlighting their advantages and disadvantages. (6 Marks)
c) The table below shows the probability distribution of a barges arriver per day at a port.
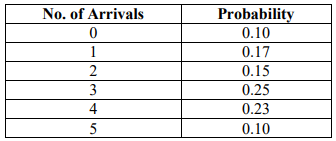
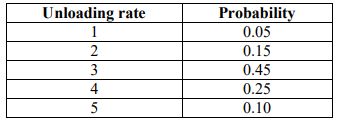
The unloading rate per day follows the probability distribution given below. NB: unloading is
done on FCFS basis.
Suppose the following are the random numbers of arrivals and random numbers of unloading.
Arrival Random No. 53, 07, 51, 82, 50, 35, 12, 57, 99, 27, 56, 93, 35, 34, 00, 22, 31
Unload Random No. 35, 66, 38, 12, 54, 75, 34, 05, 19, 70, 64, 85 90, 73, 59 61, 43
Required: Determine: simulate a seventeen day analysis and determine:
i. The average number of barges delayed (3 Marks)
ii. The average number of arrivals per day (3 Marks)
iii. The average number of barges offloaded each day (3 Marks)
QUESTION THREE: 20 MARKS
a) Define the terms verification and validation in the context of modeling. (4 Marks)
b) Dynamic systems have a state that is ever changing as a result of changes in state variables.
In your own understanding describe the terms system, system state, and state variable giving
an example from Banking system. (6 Marks)
c) Not all simulation and modeling exercises are a success. Discuss five common pitfalls to
successful simulation. (5 Marks)
d) Describe the factors that should be considered in selecting a simulation language.
(5 Marks)
QUESTION FOUR: 20 MARKS
a) State and briefly explain four properties of a good arithmetic random number generator.
(4 Marks)
b) Consider a single server queuing system. The system starts at time t=0. The arrival time of
customers is: 0.8, 1.4, 2.7, 3.2, 3.8, 8.0, 8.6, 9.0, 9.2, and 9.8. The departure times are: 2.2,
4.0, 5.0, 6.2, and 10.0. Time is in minutes. The first in first out queuing discipline is
followed. Simulate this system for six clients and estimate:
i) The average delay in the waiting line (3 Marks)
ii) The average number of clients in the waiting line at any time t (5 Marks)
iii) The expected utilization of server. (2 Marks)
c) Differentiate between the following types of models (6 Marks)
i. Deterministic Vs Stochastic Models
ii. Discrete Models Vs Continuous Models
QUESTION FIVE: 20 MARKS
a) Using the aircraft and airline systems as examples; describe all the components and
organization of a discrete event simulation models. (10 Marks)
b) Using the mid- square method obtain the first five random variables using Z0= 7182.
(5 Marks)
c) Describe the simulation clock showing its importance in the simulation model
(5 Marks)
