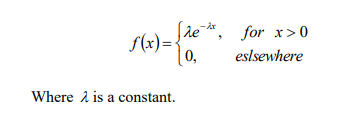UNIVERSITY EXAMINATIONS: 2018/2019
EXAMINATION FOR THE DEGREE OF BACHELOR OF SCIENCE IN
INFORMATION TECHNOLOGY / BACHELOR OF BUSINESS
INFORMATION TECHNOLOGY/ BACHELOR OF SCINCE IN APPLIED
COMPUTING
BIT2201 BBIT308 BAC2106 SIMULSTION AND MODELING
FULL TIME/PART TIME/DISTANCE LEARNING
DATE: AUGUST, 2019 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions. [30 MARKS]
a) The table below shows the number of car hijackings experienced by transport company
in a month.

(i) Using the following random number, simulate the number of car hijacking in a
period of
24
months.
Use the following random numbers:
55,82, 05, 66, 61, 02, 58, 91, 43, 31, 90, 40, 48, 64, 79, 35,17, 62, 04, 98, 63, 42,84, 33
[5 Marks]
(ii) Determine the average monthly rate of car hijacking. [1 Mark]
b) State any three types of simulation. [3 Marks]
c) Using appropriate examples identify four main types of system. [4 Marks]
d) Explain four benefits of simulation to management. [4 Marks]
e) Using the additive Linear Congruential Generator (LCG) with
a 67 , b 17 , m 31
and seed
z0 117
, generate the first five random variates on
0,1 .
[4 Marks]
f) State three shortcomings of taking a simulation approach to solve an operation research
problem. [3 Marks]
g) Describe the Monte-Carlo simulation procedure. [6 Marks]
QUESTION TWO [20 MARKS]
a) State four factors to consider when designing simulation experiment. [4 Marks]
b) Not simulation and modeling exercises are a success. Discuss five common pitfalls to
successful simulation. [5 Marks]
c) The automobile company manufactures around
150
scooters. The daily production
ranges from
146
to
154
depending upon the availability of raw materials and other
working conditions. The probability distribution is as given below:

The finished scooters are transported in a specially arranged lorry accommodating
150
scooters. Using the following random numbers:
80, 81, 76, 75, 64, 43, 18, 26, 10, 12, 65, 68, 69, 61, 57
Simulate the process to find out:
(i) What will be average number of scooters waiting in the factory? [6 Marks]
(ii) What will be average number of empty space on the lorry? [5 Marks]
QUESTION THREE [20 MARKS]
a) Draw a flow chart to describe the simulation of a simple system. [6 Marks]
b) Define the terms verification and validation in the context of modeling. [4 Marks]
c) The occurrence of rain in a city is dependent upon whether or not it rained on the previous.
If it rained on the previous day, the rain distribution is:
Event No
rain
1 cm rain 2 cm rain 3 cm rain 4 cm rain 5 cm rain
Probability
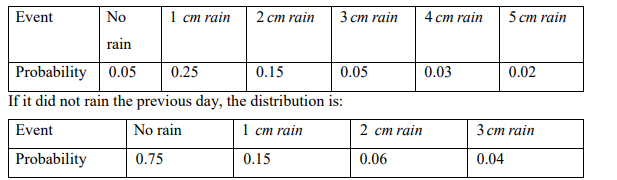
and determine by simulation the total days without rain
as well as the total rainfall during the period. Assume that for the first day of the simulation
it had rained the day before. Using the following random numbers:
67, 63, 39, 55, 29, 78, 70, 06, 78, 76
[10 Marks]
QUESTION FOUR [20 MARKS]
a) Do you think the application of simulation will strongly increase in the next ten years?
Give reasons for your answer. [10 Marks]
b) With the help of a single queueing model having inter-arrival and service time constants
1.5
and
4
minutes respectively and taking
14
minutes as the simulation period . Assume
that initially the system is empty and the first customer arrives at time
t 0.
Determine
the:
i. Average waiting time of a customer. [4 Marks]
ii. Average waiting time per customer for those who must wait.
[4 Marks]
iii. Percentage idle time of the facility. [2 Marks]
QUESTION FIVE [20 MARKS]
a) Discuss three cases when it may be necessary to use simulations. [6 Marks]
b) Describe any four statistical methods for testing the random numbers generated by the
uniform generator. [8 Marks]
c) Use the inverse transformation method to generate random variates with probability
density function. [6 Marks]