
UNIVERSITY EXAMINATION: 2018/2019
ORDINARY EXAMINATION FOR THE DEGREE IN BACHELOR OF SCIENCE IN
INFORMATION SYSTEMS SECURITY, BASIC SOFTWARE DEVELOPMENT,
BSC I.T, BBIT.
BIT1301 PROBABILITY AND STATISTICS
FULLTIME/PARTTIME/DISTANCE LEARNING
DATE: DECEMBBER 2018 TIME: 2 HOURS
INSTRUCTIONS: Answer question ONE and Any other TWO questions
QUESTION ONE (30 MARKS)
a) Distinguish between:
i. Correlation and regression (2Marks)
ii. Discrete and continuous data (2Marks)
b)
i. Find the value of b given that the harmonic mean of 2/3 b, ¼ b and 4/5 b is 4.
(2Marks)
ii. Use the three numbers in i above to show that HM < GM < AM. (3Marks)
c) The probability of getting a defective product from a factory is 0.12%. Out of 80 units randomly
selected, what is the probability that:
i. Exactly four units are defective (2Marks)
ii More than two units are defective (3 Marks)
(d) Consider the following grouped frequency distribution table
Class Interval Frequency
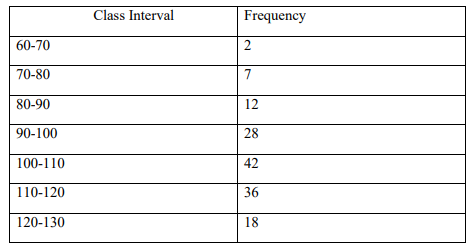
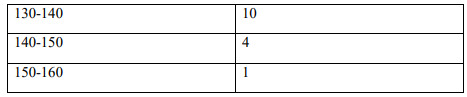
Construct:
(i) A histogram and a frequency polygon
(ii) An O-give
(iii) Estimate the median from curve (ii) above (8 Marks)
(e) A and B are two events such that
1
( / )
4
P A B
and
1
( / )
5
P B A
.Given that
P A B p ( )
find (i)
P A( ) (2 Marks)
(ii)
P B( ) (2 Marks)
(iii) Suppose
1
( )
5
P A B
find the value of
p (3Marks)
QUESTION TWO (20 MARKS)
(a) Name and explain four levels of measurements in statistics. (8Marks)
(b) A random variable X has the following probability distribution
X 0 1 2 3 4 5 6 7
f(x) 0 k 2k 2k 3k k
2 2k2 7k2+k
Find the following:
(i) The value of k.
(ii) P(X≤6)
(iii) E(x) and Var(x) (12 Marks)
QUESTION THREE (20 MARKS)
(a) Briefly describe correlation and regression analysis. (6 Marks)
(b) The table below shows a verbal reasoning test score x and an English test score, y, for each of
a random sample of 8 children who took both tests.

(i) Fit a linear regression line for prediction of the English score.
(ii) Estimate the English score given the verbal reasoning score is 115.
(iii)Compute the sample coefficient of correlation and interpret it.
(14 Marks)
QUESTION THREE (20MARKS)
(a) Define the following terms as used in statistics
(i) Statistics
(ii) Skewness
(iii) Kurtosis
(iv) Sample space
(v) Event (10 Marks)
(b) A student is likely to wake up on time with a probability
3
4
.If he wakes up on time, there is a
probability of
9
10
that he will arrive in the dinning hall in time for breakfast. If he over sleeps,
there is a probability of
1
2
that he will arrive at the dinning hall in time for breakfast. If he is late
in arriving at the dinning hall, there is a probability of
2
3
that he will miss breakfast, but on any
occasion he arrives at the dinning hall on time, he has breakfast.
(i) What is the probability that on any one day, he will miss breakfast?
(ii) If he misses breakfast, what is the probability that he woke up late?
(iii) If the student arrives late for breakfast one day, what is the probability that he woke
up late? (10 Marks)
QUESTION FIVE (20MARKS)
(a) Scores of an exam given to IT students are assumed to be normally distributed with a mean
62 and variance 6. What is the probability that:
(i) A student taking the exam scores below 66.
(ii) A student taking the exam scores between 60 and 70.
(iii) What must be the cut off point for passing exam if the examiner wants only
the top 90% of all students to pass? (10 Marks)
(b) For two frequency distributions given below, the mean from the first (f1) was 10.66 and that
from the second (f2) was 13.5. Find the value of x and y.

(10 Marks)
