 UNIVERSITY EXAMINATIONS: 2018/2019
UNIVERSITY EXAMINATIONS: 2018/2019
EXAMINATION FOR THE DEGREE OF BACHELOR OF SCIENCE IN
INFORMATION TECHNOLOGY/ BACHELOR OF SCIENCE IN
APPLIED COMPUTING/ BUSINESS INFORMATION TECHNOLOGY
BIT 1301/ BUSS 202/ BAC 1202: PROBABILITY AND STATISTICS
FULL TIME/PART TIME/DISTANCE LEARNING
DATE: AUGUST, 2019 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions.
QUESTION ONE [30 MARKS]
(a) The Marks obtained by 9 students are given below:45,32,37,46,39,36,41,48,36. Calculate
the geometric mean. [3 Marks]
(b) Differentiate between the following terms as used in statistics:
(i) A measure of skewness and a measure of kurtosis. [2 Marks]
(ii) An outcome and an event. [2 Marks]
(c) Calculate the mean, median and standard deviation of the population data below.
3, 6, 7, 1, 8, 6, 1, 7, 2, 5, 7. [5 Marks]
(d) Briefly describe stratified random sampling method. [3 Marks]
(e) Digital limited is a manufacturing company that deals in the production of soft drink
bottles. During a quality assurance exercise, it was noted that of every production lot, 0.2
per cent of soda bottles are found to be defective. The soda bottles are packed in crates
each containing 25 bottles. A soft drinks manufacturer recently bought 1,500 crates of soda
bottles from Digital Limited. Using the Poisson distribution, determine the number of
crates that will contain at least two defective soda bottles [4 Marks]
(f) The following table contains the probability distribution for the number of mobile phones
sold in small shop per day:
Number Phones Probability
0 0.25
1 0.30
2 0.20
3 0.15
4 0.10
Page 2 of 4
(i) Compute the mean number of mobile phones sold per day. [2 Marks]
(ii) Compute the standard deviation of the mobile phones sold per day. [3 Marks]
(g) For a frequency distribution, the first four moments about x=6 are 3,20,10,30 respectively.
Determine the mean, the variance, the third and fourth moments about the mean. Comment
on skewness and kurtosis of this data. (6 Marks)
QUESTION TWO [20 MARKS]
(a) The following data relates to annual profits in thousands of shillings made by an ICT
firm in different years
28 35 61 29 36 48 57 27
48 40 47 42 41 37 51 62
31 32 35 40 38 37 44 51
37 46 42 38 61 59 60 44
38 44 45 45 47 38 58 47
69 63 54 39 47 50 33 56
57 64
(i) Using a class interval of 10, construct a frequency distribution table for the data.
(4Marks)
(ii) Construct an Ogive and find the;
(a) Number of firms having profit between Ksh 37,000 and Ksh 58,000.
(b) Median profit (6 Marks)
(b)These are Marks for 20 students in an assignment
84,17,38,45,47,53, 76,54,75,22,66,65,55,54,51,44,39,19,54,72
Draw a steam and leaf diagram to illustrate the data and determine the mode.
(4Marks)
(c)The average height of 20 boys is 160cm, with a standard deviation of 4 cm. The
average height of 30 girls is 155 cm, with a standard deviation of 3.5 cm. Find the
standard deviation of the whole group. (6 Marks)
QUESTION THREE [20 MARKS]
(a) Define the following terms as used in probability.
(i) Conditional probability.
(ii) Sample space.
(iii) Mutually exclusive events.
(iv) Event. [4 Marks]
(b) Fruit seller found out that out of 40 apples in a box, 8 were bad and could not be sold.
Two fruits are drawn at random by a customer, one at a time without replacement.
(i) Find the probability that the two apples drawn are good. [3 Marks]
(ii) Find the probability that at least one of the apples is bad. [3 Marks]
(c) A husband and a wife appear in an interview for two vacancies in the same post. The
probability of a husband’s selection is 1/8 and that of the wife’s is 1/5. Find the
probability that
(i) Both of them will be selected. [2 Marks]
(ii) Only one of them will be selected. [2 Marks]
(d) A and B are two events such that
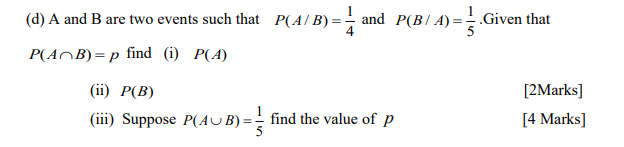
p [4 Marks]
QUESTION FOUR [20 MARKS]
The table below shows the Probability and statistics examination Marks for a class of one
hundred students in KCA university.

The mean score of the students was 46.5
(i) Show that the values of a and b are 12 and 6 respectively. (5 Marks)
(ii) Estimate the median for the above sample. (3 Marks)
(iii) Determine the variance and the standard deviation (5 Marks)
(iv) Given that 32% of the students failed the examination, what was the cut off points.
(4 Marks)
(v) Estimate the mode for this data. (3 Marks)
QUESTION FIVE [20 MARKS]
(a) As soon as a bottle of soda is opened, it begins to lose its carbonation. Fourteen 300ml
bottles of Coca-Cola were obtained, and each was assigned a randomly selected time
period (in hours). Each bottle was opened and allowed to stand at room temperature.
The carbonation (y) in each bottle was measured (in volumes) after the prescribed time
period (x). The summary statistics are given below.
![]()
(i) Find the Karl Pearson’s coefficient to correlation and interpret it.
[ 4 Marks]
(ii) The coefficient of determination and comment on its value.
[2 Marks]
(b) Morning Lighting Company is studying the relationship between kilowatt-hours
(thousands) and the number of rooms in a private single-family residence. A random
sample of 8 homes yielded the following.

You are further given that the Kilowatt-Hours depends upon the number of rooms.
(i) Determine the regression equation. [7 Marks]
(ii) Determine the estimated Kilowatt-Hours for 13 rooms. [3 Marks]
(c)The Marks of 500 IT students in an examination are normally distributed with a mean of
45 Marks and a standard deviation of 20 Marks. Given the pass mark is 40; estimate the
number of students who passed.
[4 Marks]
Number of rooms 12 9 14 6 10 8 10 10
Kilowatt-Hours (000s) 9 7 10 5 8 6 8 10
