
UNIVERSITY EXAMINATIONS: 2017/2018
EXAMINATION FOR THE DEGREES OF BACHELOR OF SCIENCE IN
INFORMATION TECHNOLOGY/ APPLIED COMPUTING/BUSINESS
INFORMATION TECHNOLOGY
BIT 1301/ BUSS 202/ BAC 1202: PROBABILITY AND STATISTICS
FULLTIME/ PART TIME/DISTANCE LEARNING
ORDINARY EXAMINATIONS
DATE: NOVEMBER, 2017 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions.
QUESTION ONE (30 MARKS)
(a)Define the following terms;
(i) Discrete random variable
(ii) Sample space
(4Marks)
(b) The mean age of 30 students in a class is 20 years. It was later discovered that while
calculating the mean, the ages of two students were wrongly taken as 21 and 20 years instead of
25 and 19 years respectively. Find the correct mean age. (4Marks)
(c) (i) Distinguish between mutually exclusive events and independent events. (4Marks)
(ii) The probability that a day is rainy is
1/4 .The probability that i carry an umbrella on a rainy
day is1/7 and that I carry an umbrella on a non-rainy day is2/7 .What is the probability that:
(i) It will not be rainy and I carry an umbrella
(ii) I shall carry an umbrella. (6Marks)
(d) From the following data.
23,25,35,41,29,50,36,37,44,30
Find the (i) Mean (1Mark)
(ii) Standard deviation (3Marks)
(iii) Inter-quartile range (2Marks)
(e) Citizen limited is a manufacturing company that deals in the production of soft drink bottles.
During a quality assurance exercise, it was noted that of every production lot, 0.2 per cent
of soda bottles are found to be defective. The soda bottles are packed in crates each
containing 25 bottles. A soft drinks manufacturer recently bought 1,500 crates of soda
bottles from Citizen Limited. Using the Poisson distribution, determine the number of
crates that will contain
(i) No defective soda bottle (3Marks)
(ii) At least two defective soda bottles (4Marks)
QUESTION 2 (20MARKS)
(a) Give five characteristics of the normal distribution. (5Marks)
(b) As a result of tests on 20,000 electric bulbs manufactured by a company. It was found
that lifetime of the bulbs was normally distributed with an average life of 2040 hours and
standard deviation 60 hours. On the basis of this information estimate the number of
bulbs that is expected to burn for:-
(i) More than 2150 hours (3Marks)
(ii) Less than 1960 hours (3Marks)
(iii) Between 2000 hours and 2270 hours. (5Marks)
(c) Distinguish between Skewness and Kurtosis (4Marks)
QUESTION 3 (20 MARKS)
(a) Distinguish between correlation and regression analysis (4 Marks)
(b) The table below shows the Marks scored by eight IT students in two tests; Probability and
Statistics(X), and Programming (Y).

Calculate Pearson’s correlation coefficient and interpret it. (8Marks)
(c) The table below shows the height and weight of a random sample of 10 patients. Use it to
answer the questions that follow
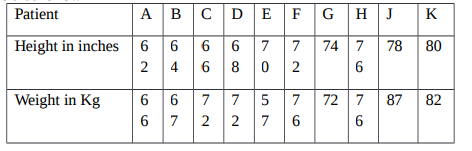
(i) Using the least squares method, determine the equation of the regression line.
(6 Marks)
(ii) Estimate the weight of a patient whose height is 71 inches. (2Marks)
QUESTION4 (20 MARKS)
(a) The following data relates to annual profits in thousands of shillings made by an ICT firm
in different years
28 35 61 29 36 48 57 27
48 40 47 42 41 37 51 62
31 32 35 40 38 37 44 51
37 46 42 38 61 59 60 44
38 44 45 45 47 38 58 47
69 63 54 39 47 50 33 56
57 64
(b) (i) Using a class interval of 10, construct a frequency distribution table for the data.
(4Marks)
(ii) Construct an Ogive and find the;
(a) Number of firms having profit between Ksh 37,000 and Ksh 58,000.
(b) Median profit (8 Marks)
(d The probability distribution of X, the number of customer arrivals per fifteen minutes period
at Otieno’s Cyber Café in Nairobi is as shown below


(i) Does the distribution meet the two requirements for probability distribution of a
discrete random variable? Justify your answer. (3Marks)
(ii) What is the expected number of customers at Otieno’s Cyber Café? (3Marks)
(2Marks)
(iii) Find P(5≤X≤9) (2Marks)
QUESTION 5 (20 MARKS)
(a)A salesman makes a sale on the average to 40% 0f the customers he contacts. If five of the
customers are contacted today, what is the probability that he makes sales to exactly two?
(4Marks)
(a) A factory produces two types of electric lamps A and B, in an experiment relating to their
life, the following results were obtained.
(i)Estimate the mean life for electric lamps A and B. (6Marks)
(ii) Estimate the standard deviation for electric lamps A and B. (6Marks)
(iii) Which electric lamp would you buy and why? (4Marks)
