
UNIVERSITY EXAMINATIONS: 2017/2018
EXAMINATION FOR THE DEGREES OF BACHELOR OF SCIENCE IN
IT/ BUSINESS IN IT/ICT/APPLIED COMPUTING
BIT1301 BBIT202 PROBABILITY AND STATISTICS
FULLTIME/ PART TIME/ DISTANCE LEARNING
ORDINARY EXAMINATIONS
DATE: APRIL 2018 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions.
QUESTION ONE [30 MARKS]
(a)Using a suitable diagram, state the difference between Skewness and kurtosis. (2Marks)
(b) The manager of a supermarket recorded the number of customers who were served at the store
between 6.00pm and 9.00pm for 12 consecutive Thursdays. The results were as follows:
285 292 243 286 301 258 286 208 215 263 252 224
Find the (i) mean (2Marks)
(ii) Median (2Marks)
(iii) Standard deviation (3 Marks)
(c) A bag contains 3 red balls and a number of black ones. The probability of drawing a red ball from the
bag is 0.2. How many balls are there in the bag? (3Marks)
(d)Measurements of air velocity(x) and evaporation (y) of burning fuel droplets in a impulse
engine gave the following quantities.
![]()
(i) Determine the least squares regression line of y on x i.e. y=ax + b. (4Marks)
(ii) Estimate the evaporation coefficient of a droplet when air velocity is 190. (1Mark)
(e)The table below shows the performance of various drivers in a car rally.
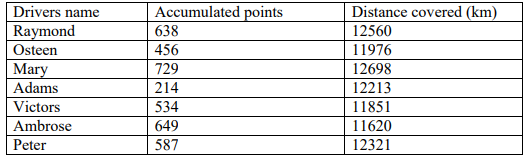
Determine the rank correlation coefficient for this information and interpret it
(6Marks)
(f) 5% of all TVS manufactured by a large electronic company are defective; a quality control
inspector randomly selected three TV’s from the production line. What is the probability that
exactly one of these three TV’s is defective? . (4 Marks)
(g) The average income for a group of 50 persons working in a factory was calculated to be
Ksh169. It was later discovered that one figure was misread as 134 instead of the correct value
Ksh143. Calculate the correct average income. [3 Marks]
QUESTION TWO (20 MARKS)
(a) Distinguish between ‘correlation ‘and ‘regression’. (4Marks)
(b) From the given data on Marks obtained by 10 IT students in programming and Statistics, find the
correlation coefficient and interpret it.
![]()
(6 Marks)
(c) The table below shows the investments of a certain company in advertisement from the year 1996
to 2004 and the corresponding sales within the same period.
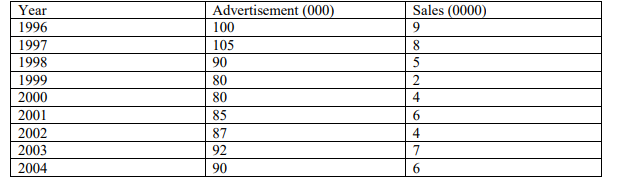
(i) By use of a scatter diagram investigate the relationship between investment in
advertisement and sales. (4 Marks)
(ii) Fit a regression equation of investment in advertisement on sales (6Marks)
QUESTION THREE (20MARKS)
(a)The number of passengers in a car in a freeway has the probability mass function given by

(i) Does the distribution meet the two requirements for probability distribution of a
discrete random variable? Justify your answer. (3Marks)
(ii) Find the expected number of passengers in a car. (3Marks)
(iii) Calculate the standard deviation of the number of passengers in a car. (4Marks)
(c) A student at Nairobi Campus is likely to wake up on time with probability
3/4
.If he
wakes up on time, there is a probability of
9/10
that he will arrive in the dining hall in time
for breakfast. If he oversleeps, there is a probability of
1/2
that he will arrive at the dining
hall in time for breakfast. If he is late in arriving at the dining hall, there is a probability of
2/3
that he will miss breakfast, but on my occasion he arrives at the dining hall on time he has
breakfast
(i) What is the probability that on any one day, he will miss breakfast?
(ii) If he misses breakfast, what is the probability that he woke up late?
(iii) If the student arrives late for breakfast one day, what is the probability
that that he woke up late? (10
Marks)
QUESTION FOUR (20MARKS)
(a) Given below are the daily wages paid to workers in two factories X and Y.
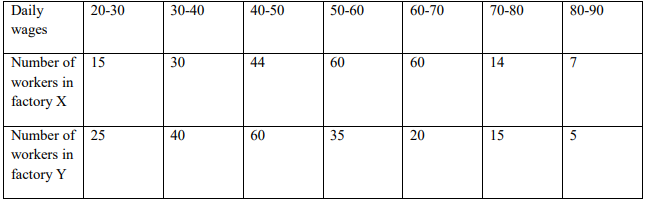
(i) Which factory pays higher average wages? By how much? (5Marks)
(ii) In which factory are the wages more variable? (5Marks)
(iii) Which factory has to pay more wages in a month assuming that both work for 25 days in a
month? (5Marks)
(b) If the probability that a husband will be alive in 50 years is 0.4 and the probability that the wife will be
in 50 years is 0.7. Find the probability that
(i) Both will be alive. (2Marks)
(ii) None will be alive (3Marks)
QUESTION FIVE (20 MARKS)
(a) The heights of 300 patients are normally distributed with mean 68.0 inches and variance 9.
How many patients have heights;
(i)Greater than 72 inches. (3Marks)
(ii) Between 65 and 72 inches. (4Marks)
(b)The table below shows the Marks out of 50, obtained by 80 it students in BMA 1104 examination.

Using the data
(i)Find the mean of the distribution (2Marks)
(ii) Find the variance (3Marks)
(iii) Plot a ‘less than ‘cumulative frequency polygon(Ogive), hence determine the median for
the distribution using the ogive (4 Marks)
(iv) Plot a histogram, hence using the histogram determine the mode for the distribution.
(4Marks)
