 UNIVERSITY EXAMINATIONS: 2016/2017
UNIVERSITY EXAMINATIONS: 2016/2017
EXAMINATION FOR THE DEGREE OF BACHELOR OF SCIENCE IN
INFORMATION TECHNOLOGY
BIT1301 BAC1202 BUSS 202 PROBABILITY AND STATISTICS
FULL TIME & PART TIME
SPECIAL/SUPPLEMENTARY EXAMINATION
DATE: JULY, 2017 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions.
QUESTION ONE – COMPULSORY (30 MARKS)
(a) Define the following terms;
(i) Statistics
(ii) Probability
(iii) Independent events (6 Marks)
(b) The mean age of 30 students in a class is 20 years. It was later discovered that while
calculating the mean, the ages of two students were wrongly taken as 21 and 20 years instead
of 25 and 19 years respectively. Find the correct mean age. (4 Marks)
(c) A student is likely to wake up on time with a probability
3/4
.If he wakes up on time, there is a
probability of
9/10
that he will arrive in the dinning hall in time for breakfast. If he over sleeps,
there is a probability of
1/10
that he will arrive at the dinning hall in time for breakfast. If he is
late in arriving at the dinning hall, there is a probability of
2/3
that he will miss breakfast, but on
any occasion he arrives at the dinning hall on time, he has breakfast.
(i) What is the probability that on any one day, he will miss breakfast?
(ii) If he misses breakfast, what is the probability that he woke up late?
(iii) If the student arrives late for breakfast one day, what is the probability that he
woke up late?
(8 Marks)
(d) From the following data.
23,25,35,41,29,50,36,37,44,30
Find the:
(i) Mean (2 Marks)
(ii) Standard deviation (3 Marks)
(iii) Inter-quartile range (3 Marks)
(e) The table below shows the relative prices of rice and wheat in Tatu supermarkets.
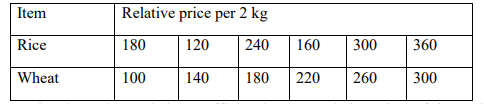
Determine the rank correlation coefficient between relative prices of rice and wheat.
(4 Marks)
QUESTION TWO (20 MARKS)
(a) Using appropriate diagrams, briefly explain the following types of distributions:
(i) Platykurtic distribution (2 Marks)
(ii) Leptokurtic distribution (2 Marks)
(b) Scores of an exam given to IT students are assumed to be normally distributed with a mean
62 and variance 6.What is the probability that:
(i) A student taking the exam scores below 66.
(ii) A student taking the exam scores between 60 and 70.
(iii) What must be the cut off point for passing exam if the examiner wants only
the top 90% of all students to pass? (12 Marks)
(c) A salesman makes a sale on the average to 40% 0f the customers he contacts. If five of the
customers are contacted today, what is the probability that he makes sales to exactly two?
(4 Marks)
QUESTION THREE (20 MARKS)
(a) Distinguish between correlation and regression analysis (4 Marks)
(b) The table below shows the marks scored by eight students in two tests; Probability and
Statistics(X), and Programming (Y).
X 67 42 85 51 39 97 81 70
Y 70 59 71 38 55 62 80 76
Calculate Pearson’s correlation coefficient and interpret it. (8 Marks)
(c) The following data were obtained from the sales records of Umoja motors, a second
hand motor vehicle dealer:
Age of motor
vehicle(years)
7 9 8 14 9 7 9 10 5 8
Selling
price(Sh’000’)
700 495 450 380 485 720 560 450 1,250 650
Using ordinary least squares equation, estimate the selling price of a six year old motor
vehicle (8 Marks)
QUESTION FOUR (20 MARKS)
(a) The following data relates to annual profits in thousands of shillings made by an ICT firm
in different years
28 35 61 29 36 48 57 27
48 40 47 42 41 37 51 62
31 32 35 40 38 37 44 51
37 46 42 38 61 59 60 44
38 44 45 45 47 38 58 47
69 63 54 39 47 50 33 56
57 64
(i) Using a class interval of 10, construct a frequency distribution table for the data.
(4 Marks)
(ii) Construct an Ogive and find the;
(a) Number of firms having profit between Ksh 37,000 and Ksh 58,000.
(b) Median profit (8 Marks)
(b) The probability that an individual will suffer a bad reaction from an injection of a given
serum is 0.001.Determine the probability that out of 2000 individuals 2 individuals will suffer
a bad reaction. (3 Marks)
(c) In a certain statistical distribution, the following results were obtained
Arithmetic mean
X 45
Median M
d
=48
Coefficient of Skew ness=-0.4
Calculate
(i) Mode
(ii) Standard deviation (5 Marks)
QUESTION FIVE (20 MARKS)
(a) Explain briefly two data collection methods. (4 Marks)
(b) A factory produces two types of electric lamps A and B, in an experiment relating to their
life, the following results were obtained.
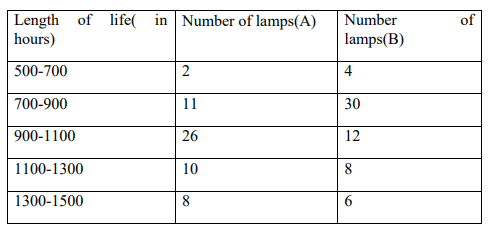
(i)Estimate the mean life for electric lamps A and B. (6 Marks)
(ii) Estimate the standard deviation for electric lamps A and B. (6 Marks)
(iii) Which electric lamp would you buy and why? (4 Marks)