
UNIVERSITY EXAMINATIONS 2016/2017
ORDINARY EXAMINATION FOR BACHELOR OF INFORMATION TECHNOLOGY
BIT1206 DISCRETE MATHEMATICS (DAY/EVENING)
DATE: AUGUST, 2017 TIME: 2 HOURS
INSTRUCTIONS: Answer question ONE and Any other TWO questions
QUESTION ONE
(a) Describe the Boolean Algebra B with two elements, 0 and 1 called bits. (3 Marks)
(b) (i) Define the dual of any statement ? in a Boolean algebra B. (1 Mark)
(ii) Write the dual of each Boolean equation

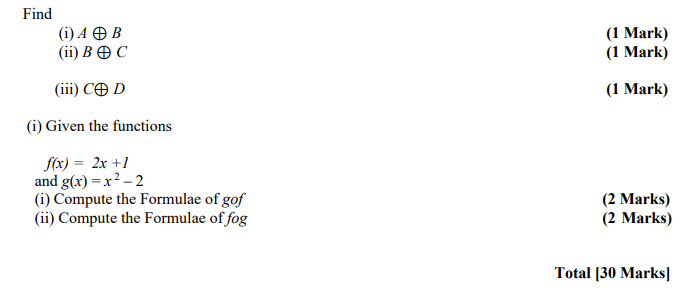
QUESTION TWO
a) (i) Define a multigraph. (2 Marks)
(ii) Consider the graph G = G(V, E ) shown below
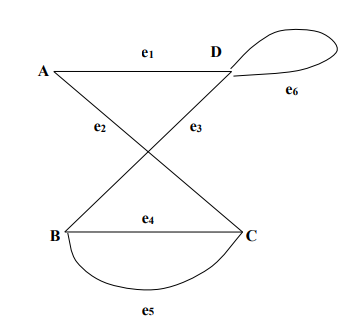
Find the number of verticles and edges (4 Marks)
(iii) In a(ii) are there any multiple edges or loops? If so, what are they? (4 Marks)
(b) Consider a graph G where
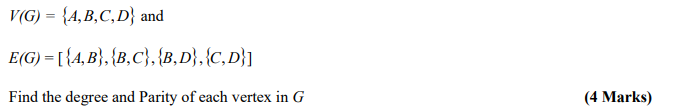
(C) (i) Define a path and a trail in a graph (multigraph) G. (2 Marks)
(ii) Let G be the graph below
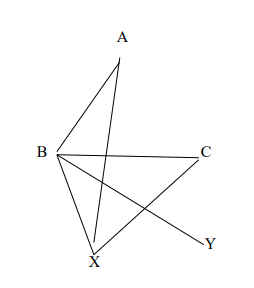
determine whether each of the following is a closed path, trail, simple path or a cycle
(a) (B,A,X,C,B,Y) (1 Mark)
(b) (X,C,A,B,Y) (1 Mark)
(c) (X,B,A,X,C) (2 Marks)
Total[20 Marks]
QUESTION THREE
(a) Prove that
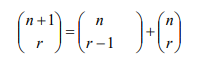
(b) Suppose that repetitions are not permitted
(i) How many three digit numbers can be formed from the digits 2, 3,4,5,7 and 9 (2 Marks)
(ii) How many of these numbers are less than 400? (2 Marks)
(iii) How many are even? (2 Marks)
(iv) How many are odd? (2 Marks)
(v) How many are multiples of 5? (2 Marks)
(c) Find the number of ways that five large books, four medium sized books and three small books
can be placed on a shelf so that all books of the same size are together. (2 Marks)
(d) How many committees of five with a given chairperson can be selected form twelve persons?
(3 Marks)
(e) In how many ways can three or more persons be selected from twelve persons? (2 Marks)
Total [20 Marks]
QUESTION FOUR
a) In a survey of60people it is found that25like to drink milk,25drink coffee, and26tea.9like milk and tea,11like milk and coffee,8
like coffee and tea and8like none of thethree.
i. Find the number of people who like all the three drinks (3 Marks)
ii. Use the value obtained in (i) to represent information in a Venn-diagram.
(4 Marks)
iii. Find the number of people who like exactly one of the three drinks (2 Marks)
iv. Find the number of people who like atleast one of the three drinks (2 Marks)
v. Find the number of people who like milk and coffee but not tea.
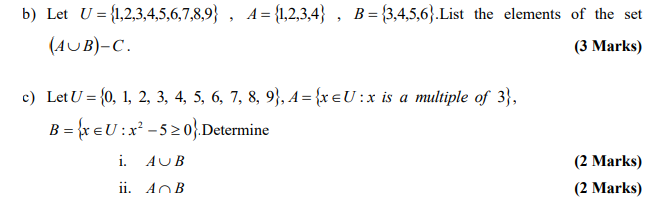
QUESTION FIVE
(a) Define the following terms
(i) Proposition (1 Mark)
(ii) Tautologies (1 Mark)
(iii) Contradictions (1 Mark)
(iv) An argument (1 Mark)
(v) A fallacy (1 Mark)
(b) Determine the validity of the argument
![]()
(c) Test the validity of the following argument
If i study, then i will not fail mathematics.
If i do not play basketball, then i will study.
But i failed mathematics
…………………………………………………………………………………………………………………………………………
Therefore i played basketball (4 Marks)
(d) Show that p ↔ ∼ q does not logically imply p → q (4 Marks

