 UNIVERSITY EXAMINATIONS 2018/2019
UNIVERSITY EXAMINATIONS 2018/2019
ORDINARY EXAMINATION FOR BACHELOR OF SCIENCE INFORMATION
TECHNOLOGY, BSc. APPLIED COMPUTING, BSD, BISF
BIT 1206: DISCRETE MATHEMATICS (DAY/EVENING)
DATE: APRIL, 2019 TIME: 2 HOURS
INSTRUCTIONS: Answer question ONE and Any other TWO questions
QUESTION ONE
a) In a Boolean algebra, the following are equivalent:
(1) ? + ? = ?
(2) ? ∗ ? = ?
(3) ?′ + ? = 1
(4) ? ∗ ?′ = 0
Prove the equivalence of (1) and (2) (4 Marks)
b) Write the dual of each Boolean equation
i) (? + ?)(? + ?) = ?? + ? (2 Marks)
ii) (? + 1)(? + 0) = ? (2 Marks)
c) Test the validity of the following argument:
If it rains, Erick will be sick.
It did not rain.
Erick was not sick. (8 Marks)
d) Show that p ˄ q logically implies p ↔ q (4 Marks)
e) Consider a graph where
V (G) = {A, B, C,D} and
E (G) = [{A, B},{B, C},{B,D},{C,D}]
Find the degree and parity of each vertex in G (4 Marks)
f) Let:
U = {1, 2, 3, … . .8, 9}
A = {1, 2, 3, 4}
B = { 2, 4,6,8}
C= { 3, 4,5,6} be sets
Find
i) A ∪ B (3 Marks)
ii) B ∩ C (3 Marks)
Total [30 Marks]
QUESTION TWO
a) Define the following terms
i) One-to-one (or injective ) Functions (2 Marks)
ii) Onto (or surjective) Functions (1 Mark)
iii) One-to-one correspondence (or bijective) Functions (2 Marks)
iv) Invertible Functions (2 Marks)
b) Write the negation of each of statement as simply as possible
i) If he studies, he will pass the exam (3 Marks)
ii) He swims if and only if the water is warm. (3 Marks)
iii) If it snows, then he does not drive the car. (3 Marks)
c) Let ? denote, “He is rich” and let ? denote, “He is happy”. Write each statement in symbolic
form
i) Being rich is a necessary condition to being happy (1 Mark)
ii) One is never happy when one is rich (1 Mark)
iii) He is poor only if he is happy (1 Mark)
iv) To be rich means the same as to be happy (1 Mark)
Total [20 Marks]
QUESTION THREE
(a) Draw the multigraph G whose adjacency matrix A is A =
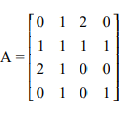
(5 Marks)
(b) Let G be the graph where
V (G) = {A, B, C, X, Y, Z} and
E (G) = [{A, C}, {A, X}, {A, Y}, {B, Y}, {B, Z}]
i) Find G-A (2 Marks)
ii) Determine the number of connected components of G-A (2 Marks)
(c) Draw a diagram of each of the following graphs G (V, E):
i) V = {A, B, C, D}
E = [{A, B}, {A, D}, {B, C}, {B, D}, {C, D}] (2 Marks)
ii) V= {a, b, c, d, e}
E= [{a, b}, {a, c}, {b, c}, {d, e}] (2 Marks)
d) Determine the contrapositve of each statement.
i) If he has courage he will win. (1 Mark)
ii) It is necessary to be strong in order to be a sailor. (1 Mark)
iii) Only if he does not tire will he win. (1 Mark)
iv) It is sufficient for it to be a square in order to be a rectangle. (1 Mark)
v) Prove: (p → q) if ? is an integer and ?
2
is odd, then ? is odd (3 Marks)
Total [20 Marks]
QUESTION FOUR
a) List the elements of the following sets
i) A = {?: ? ∈ ?, 3 < ? < 9} (1 Mark)
ii) B = {?: ? ∈ ?, ?
2+1 = 10} (1 Mark)
iii) C = {?: ? ∈ ?, ? is odd , −5 < ? < 5} ` (1 Mark)
b) i) Draw a Venn diagram of sets A, B, C where A ⊆ B, sets A and C are disjoint
but B and C have elements in common (4 Marks)
ii) Write A ∩ (B ∪ C) as the (disjoint) union of fundamental products. (5 Marks)
c) Let G be the graph below:
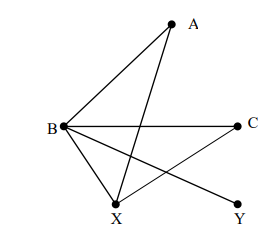
Determine whether each of the following is a closed path, trail, simple path or cycle.
i) (B, A, X, C, B), (1 Mark)
ii) (X, A, B, Y), (1 Mark)
iii) (B, X, Y, B). (1 Mark)
C B
X Y
A
4
d)
i) Define the subgraph G – e where e is an edge in G (1 Mark)
ii) Define a bridge for a connected graph G (1 Mark)
iii) Let G be the graph below.
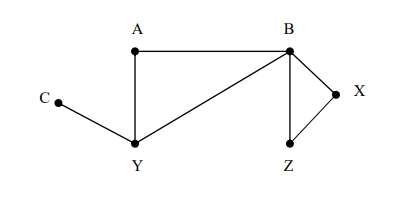
Find:
a) G – X (1 Mark)
b) G – Y (1 Mark)
c) G – Z (1 Mark)
Total [20 Marks]
QUESTION FIVE
a) How many Diagonals does a regular polygon with ? sides have? (5 Marks)
b) Which regular polygon has the same number of diagonals as sides? (5 Marks)
c) Find the number ? of triangles that can be formed by the vertices of a regular
polygon with n sides (and hence ? vertices) (5 Marks)
d) Find the number ? of triangles that can be formed by the vertices of a regular polygon with ?
sides (and hence ? vertices) if the sides of the polygon are not to be sides of any
triangle. (5 Marks)
Total [20 Marks]
