 UNIVERSITY EXAMINATIONS: 2011/2012
UNIVERSITY EXAMINATIONS: 2011/2012
SECOND YEAR EXAMINATION FOR THE BACHELOR OF
SCIENCE IN INFORMATION TECHNOLOGY
BIT 3101A 2102 DATA STRUCTURES AND ALGORITHIMS
DATE: AUGUST, 2012 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE
a) Define the following terms:
i. Algorithm
ii. Spanning tree
iii. Miniheap and
iv. Selection sort
[4 Marks]
b) State four advantages of implementing data structures as abstract data types
[4 Marks]
c) i. State under what conditions you would choose an array-based
implementation for the stack and also under what conditions would you
choose a pointer-based implementation. [4 Marks]
ii. If you push the letters D, C, B and A in order onto a stack of characters
and then pop them, in what order will they be deleted from the stack?
[2 Marks]
d) Define a recursive function and give any two examples that can be solved
recursively. [2 Marks]
e) The numbers 10, 72, 86, 95,30,15,90,70,60,85 are to be stored for some
processing in that order. Write down the order in which the numbers will be
printed if they are:(i) stored in a queue (ii) stored in a stack and (iii) stored in a
binary search tree and traversed in order.
[8 Marks]
f) i. State a necessary and sufficient condition for a graph to have a spanning
tree. [2 Marks]
ii. Explain how Prims’ algorithm finds a minimal spanning tree [2 Marks]
iii. True or False. If all the weights in a connected graph G are distinct,
distinct spanning trees of G have distinct weight. [2 Marks]
QUESTION TWO
a) When sorting an array by using mergesort
i. Do the recursive calls to mergesort depend on the values in the array, the number
of items in the array, or both? Explain. [3 Marks]
ii. In what step of mergesort are the items in the array actually swapped (i.e. sorted)?
Explain. [3 Marks]
b) i. A pointer based implementation of a list require more memory than a
array- based implementation. Explain. [2 Marks]
ii. A circular doubly linked list eliminates special cases for insertion and
deletion. Explain [2 Marks]
c) Suppose you have a sorted array and you use a binary search to determine
Whether a given integer occurs in the array. Next you display all the
integers in the sorted array. which algorithm is faster, in general, the
binary search or displaying the integer? Explain in terms of the Big O
notation [3 Marks]
d) i. Explain how the divide and conquer technique works. [3 Marks]
ii. What is a base case in a recursive procedure? Explain why every recursive
procedure must have a base case. [4 Marks]
QUESTION THREE
a) Define the following terms with respect to graphs:
i. Connected graph
ii. Degree of a vertex
iii. Cycle and
iv. Simple path
[4 Marks]
b) Represent the following expression tree: (((A+B)*C+D)*E)-((A+B)*C-D) and
write the prefix and postfix expressions. [6 Marks]
c) i. Describe Dijkstras shortest-path problem. [2 Marks]
ii. State necessary and sufficient condition that a graph has a path with no
repeated edges from v to w(v ≠ w) containing all the edges and vertices.
[2 Marks]
d) Let T be a tree connected by Dijkstra’s algorithm in the process of solving the
single-source shortest path problem for a weighted connected graph G. True or
false:
i. T is a spanning tree of G
ii. T is a minimum spanning tree of G.
[2 Marks]
e) i. Distinguish between preorder and postorder traversal [2 Marks]
ii. Give example of distinct binary trees B1 and B2, each with two vertices,
with preorder vertices listing of B1 equals to the post-order listing of B2.
[2 Marks]
QUESTION FOUR
a) Suppose that you have a stack S and an empty auxiliary stack T. Show how you
can do each of the following tasks by using only the ADT stack operations
i. Display the contents of S in reverse order; that is, display the top last. [3 Marks]
ii. Count the number of items in S, leaving S unchanged. [3 Marks]
iii. Delete every occurrence of a specified item from S, leaving the order of the
remaining items unchanged. [3 Marks]
b) For large arrays and in the worst case, is selection sort faster than insertion sort.
Explain. [2 Marks]
c) The factorial function can be defined can be defined by the recurrence relation
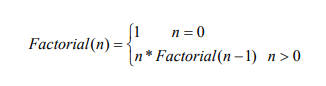
Factorial n
i. Write down the C++ function that implements the definition indicating the
preconditions and post conditions. [3 Marks]
ii. Demonstrate that the function in (i) is recursive by listing the criteria of a
recursive solution and stating how the function meets each criterion. [6 Marks]
QUESTION FIVE
a) i. How do binary search works. What properties must the input have?
[4 Marks]
ii. Estimate how many times faster an average successful search will be in a
sorted array of 100,000 elements if it is done by binary search versus
sequential search [4 Marks]
b) What is the order of each of the following tasks in the worst case? [4 Marks]
i. Displaying all N integers in an array
ii. Displaying the last integer in a linked list.
iii. Adding an item to a stack of N items
iv. Adding an item to a queue of N items
c) i. Beginning with an empty binary search tree, what binary search tree is
formed when you insert the following values in the order given W I L B E
R F O R C E [3 Marks]
ii. Show the results of traversing the BST of (i) above in inorder. [2 Marks]
d) What is the order of magnitude for the following expression? [3 Marks]
i n ii n n n2
![]()
