
UNIVERSITY EXAMINATIONS: 2018/2019
EXAMINATION FOR THE DEGREE OF BACHELOR OF SCIENCE IN
INFORMATION TECHNOLOGY
BIT 2301A: COMPUTER GRAPHICS
FULL TIME/PART TIME/DISTANCE LEARNING
DATE: APRIL, 2019 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions.
QUESTION ONE (30 MARKS)
a) The architecture of a raster-graphics system is partly made up of the components listed below.
Briefly explain the function of the following components and terms as used in image
formation and display in the display device.
i. Display processor
ii. Frame Buffer
iii. Scan Conversion
iv. Video Controller
v. Display Processor Memory
(2 Marks Each)
b) Why are matrix representations used to describe point transformations in computer graphics?
(4 Marks)
c) Describe how to represent three different 2D transformations as matrices. (4 Marks)
d) Explain how to derive a sequence of transformations to achieve the overall effect of
performing a 2D rotation about an arbitrary point. (4 Marks)
e) Consider the following figure:
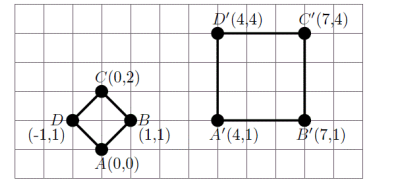
2010 Paper 4 Question 4
Computer Graphics and Image Processing
(a) Homogeneous coordinates are often used to represent transformations in 3D:
QUESTION TWO (20 MARKS)
The most popular technique used in computer animation is the key frame interpolation technique or
in-betweening.
Consider an object with its local origin at an initial position Pin = (Xin,Yin,Zin) at key frame KFin,
which then attains the final position of Pfin =(Xfin, Yfin’ Zfin) at keyframe KFfin.
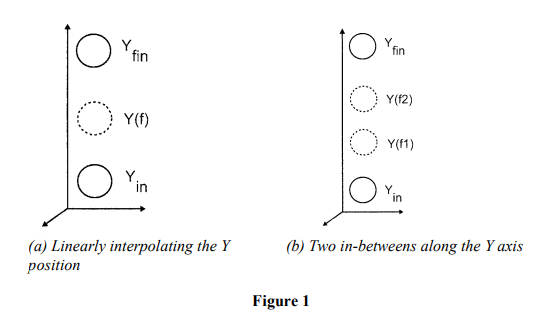
Assuming that you want one in between frame as in figure (a), using linear interpolation what
is the position of Y(f).
(5 Marks)
b) Now suppose we needed two in-between frames, Fi and Fj as shown in figure (b), Determine
the coordinates of the two in- between frames.
(5 Marks)
c) If we were to extend the above to a total of N frames (including the initial and final key
frames), we would have N-2 in-between frames. Give the equation of the position of any
frame J .
(10 Marks)
Linear Interpolation
The simplest type of interpolation is linear interpolation. In linear interpolation,
the values of a given property is estimated between two known values on a
straight-line basis (hence the term linear). In simpler terms, linear interpolation
takes the sum of the property values in the two key frames and divides by the
number of frames needed to provide as many equally spaced in-between frames
as needed. For example, consider a model P, with a position along the y-axis of
Yi, at the initial key frame Kin. At the final key frame, Kfin, they position has
moved to Yfin. Now, say we want only one in-between frame f. This frame would
be midway between the two key frames, and P would be located midway
between the positions Yi, and Yfin as shown in Fig.9.3.
Fig.9.3: Linearly interpolating the Y position
Mathematically, the position Y(f) at Frame f, is given by
YO = Yin + (Ylin – Yi,J / 2 = + YiJ / 2
Now, suppose we want two in-between frames, fl and f2. The model would
then be defined such that at fly it occupies a position, Y(fl), which is one third
the distance from Yin; and at frame f2, it occupies a position Y(f2), which is two
thirds the distance from Yin.
QUESTION THREE (20 MARKS)
a) EXPLAIN 2 (Two) ways that Linear Algebra is used in Computer Graphics discipline.
(4 Marks)
b) OUTLINE the key stages in the processes involved in the production of a 3D full feature
animated movie.
(10 Marks)
c) EXPLAIN ways by which these steps differ between production of animated Movie and
Computer Game development.
(6 Marks)
QUESTION FOUR (20 MARKS)
Three-dimensional objects can be grouped together to create structures that define how these models
are transformed and how they relate to one another. Grouping of these models creates structures
called hierarchical structures, because within these structural groupings some objects are always more
dominant than others. The components of the structure are commonly referred to as nodes.
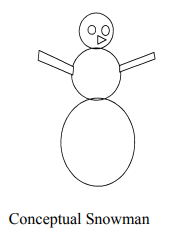
The figure below shows a conceptual snowman. It has the following components; the base, tummy,
and head are of course all spheres. The hands are cylinders, the eyes are disks, and the carrot-shaped
nose is a simple cone.
Using a diagram, DEFINE the hierarchy of the Snowman.
QUESTION FIVE (20 MARKS)
a) Briefly DISCUSS each of the following concepts. Clearly explaining its relevance in
computer graphics image formation.
i. Lighting
ii. Shading
iii. Illumination
iv. Ray Tracing
(3 Marks each)
b) Using a flow chart, EXPLAIN the DDA line drawing algorithm
