 UNIVERSITY EXAMINATIONS: 2017/2018
UNIVERSITY EXAMINATIONS: 2017/2018
EXAMINATION FOR THE DEGREES OF BACHELOR OF SCIENCE IN
INFORMATION TECHNOLOGY/ APPLIED COMPUTING
BIT 2301 A/ BAC 3206: COMPUTER GRAPHICS
FULLTIME/ PART TIME
ORDINARY EXAMINATIONS
DATE: AUGUST, 2018 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions.
QUESTION ONE [30 MARKS]
a) Computer graphics comprises THREE basic elements. Explain each of them. (6 Marks)
b) Explain the operation of the cathode ray tube. (4 Marks)
c) Describe the following primitives used in computer graphics:
i) Vertex (1 Mark)
ii) Line (1 Mark)
iii) Face (1 Mark)
d) Explain how the raster scan is used to display objects on the screen. (4 Marks)
e) Describe any FOUR factors in a typical illumination model. (4 Marks)
f) The A-buffer expands on the depth buffer method to allow transparencies. Required:
i) Identify the key data structure used by the A-buffer method (1 Mark)
ii) Describe the TWO fields used by the A- buffer (4 Marks)
iii) The surface buffer in the A-buffer includes several components, name
any FOUR of these components (4 Marks)
QUESTION TWO [20 MARKS]
a) Explain and illustrate the following terms related to 2D viewing:
i) Window
ii) Viewport (6 Marks)
b) Discuss any TWO day-to-day graphics operations that result in transformations between the
window and viewport. (4 Marks)
c) Identify and briefly discuss ONE approach to each of the following forms of 2D clipping:
i) Line clipping (2 Marks)
ii) Fill-area clipping (2 Marks)
iii) Text clipping (2 Marks)
d) Discuss the ‘back-face-detection’ method of hidden surface elimination. (4 Marks)
QUESTION THREE [20 MARKS]
a) Describe the following graphics display terms: (6 Marks)
i) Mirror line
ii) DAC
iii) Aliasing
b) The digital differential analyzer is the simplest line drawing algorithm, but has TWO key
limitations. Briefly discuss these limitations. (2 Marks)
c) Apply the Bresenham line drawing algorithm to discover the intermediate points between the
following sets of points:
i) (5,8) and (16,13) (4 Marks)
ii) (2,5) and (5,11) (4 Marks)
iii) (4,3) and (12,8) (4 Marks)
QUESTION FOUR [20 MARKS]
a) During illumination, computer graphics considers THREE kinds of surfaces:
i) Specular surface
ii) Diffuse surface
iii) Translucent surface
Discuss how each of these surfaces interact with light and give examples of each surface.
(6 Marks)
b) Distinguish between global and local illumination and draw a diagram to illustrate
each type. (4 Marks)
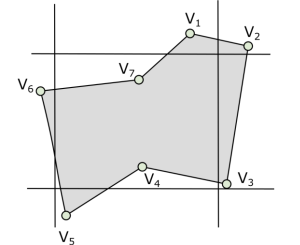
c) Consider the shape below that needs to be clipped using the Sutherland-Hodgman
algorithm. Illustrate the clipping process clearly showing the steps, and present the clipped
hexagon with its new set of vertices (6 Marks)
d) Describe any TWO shading models. (4 Marks)
QUESTION FIVE [20 MARKS]
a) Consider a polygon with the vertices (1,5) (1,2) (3,1) (5,7) (6,5) (1,5). Showing all your
calculations, calculate and plot the new vertices after it has undergone the following
transformations on a 2D plane:
i) A translation of (3,-6) (3 Marks)
ii) A scaling of (0.5,2) (3 Marks)
iii) A rotation of 90ᵒ clockwise about the origin (3 Marks)
Plot the original and transformed polygons on a Cartesian plane. (4 Marks)
b) Describe FOUR conditions that must be met for a point NOT to be clipped. (4 Marks)
c) Discuss the ‘rendering equation’ and its associated problem. (3 Marks)
