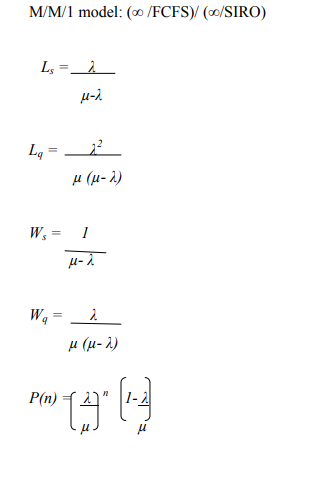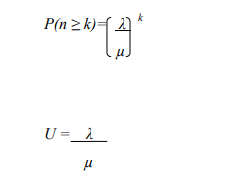UNIVERSITY EXAMINATIONS: 2011/2012
SECOND YEAR EXAMINATION FOR THE BACHELOR OF
SCIENCE IN INFORMATION TECHNOLOGY
BIT 2207 OPERATIONS RESEARCH
DATE: AUGUST, 2012 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE
a) List any three basic requirements of a Linear programming model (3 Marks)
b) Using an appropriate example explain Degeneracy in a Transportation problem.
How would you resolve the degeneracy? (3 Marks)
c) State any two types of solutions generated from Integer programming methods.
(2 Marks)
d) Explain any three advantages and two limitations of Simulation. (5 Marks)
e) A fleet owner finds from his past records that the costs per year of running vehicle
whose purchase price is K£ 50,000 are as follows:
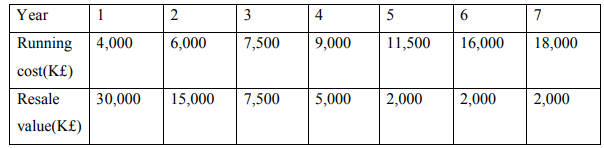
Thereafter, running costs increase by K£2,000 per year but the resale value
remains steady at K£2,000.At what age is the replacement due? (10 Marks)
f) Seven jobs, each of which has to go through the machines M1 and M2 in the order
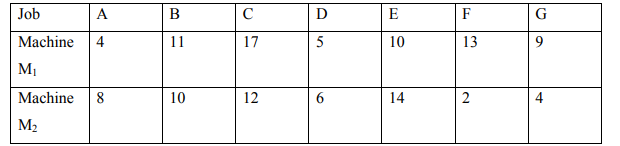
Determine the optimal sequence that will minimize the total elapsed time and idle
times of each machine.
(7 Marks)
QUESTION TWO
A bank plans to open a single-server drive- in banking facility at a particular centre. It is
estimated that 28 customers will arrive each hour on average. On average, 2 minutes are
required to process a customer’s transaction. Assuming Poisson arrivals and exponential
service, determine,
a) The proportion of time the server will be idle, (3 Marks)
b) On average, how long a customer will have to wait for service, (3 Marks)
c) The length of drive way required to accommodate all the arrivals, on average, if
20 feet drive way is required for each car waiting for service, (5 Marks)
d) The average time a customer spends in the system. (3 Marks)
e) The probability that a customer arriving at the facility will have to wait. (3 Marks)
f) The probability that there will be at least 10 cars in the system at any time.
(3 Marks)
QUESTION THREE
a) Explain looping and dangling as used in the context of Network analysis.
(4 Marks)
b) The following table lists data for a PERT network:
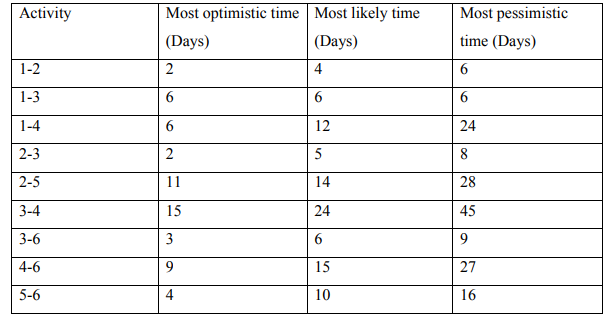
i. Compute the expected time for each activity. (3 Marks)
ii. Draw the project network. (3 Marks)
iii. Estimate the earliest and latest event times for all nodes and hence derive the
critical path and the expected project duration. (6 Marks)
iv. What is the probability that the project duration will exceed 62 days (4 Marks)
QUESTION FOUR
a) Explain the following terminologies as used in theory of Games:
i. Minimax and maximin principles (4 Marks)
ii. Two person zero sum game (2 Marks)
iii. Dominance properties (4 Marks)
iv. Saddle point game (2 Marks)
b) Two leading suppliers, firm A and firm B are the only suppliers of computer
equipment in a remote town in North Eastern Kenya. With an increasing demand
for their products each has plans for future activities such as not to expand,
change the present size of the stores, or to open additional branches in the
province. The pay-off matrix to the firm A in terms of percentage gain or loss is
given below:
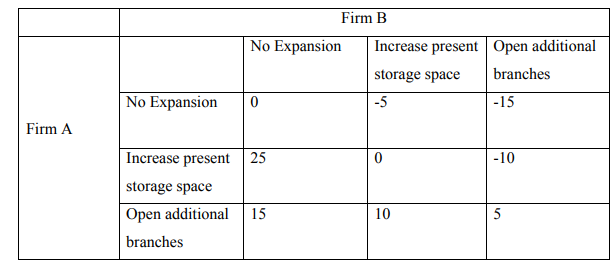
Determine the optimal strategies for the two firms. (8 Marks)
QUESTION FIVE
a) What is an “unbalanced” Assignment problem? Explain how this problem could
be tackled. (3 Marks)
b) Find an optimal assignment for an assignment problem with the following cost
matrix using the Hungarian Assignment method:
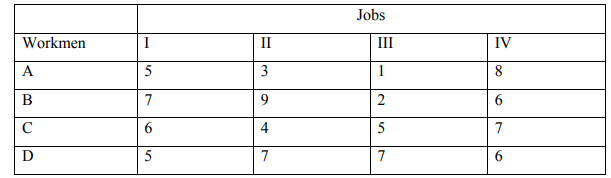
(7 Marks)
c) A company uses 42,000 units per year of an electronic component each costing
K£2. Placing each order costs K£100 and the carrying cost is 20% per year of the
average inventory.
i. Find the EOQ. (3 Marks)
5
ii. If the company gets 5% discount on single order, should it accept the discount
offer? (7 Marks)
APPENDIX
Queuing Formulae
