 UNIVERSITY EXAMINATIONS: 2010/2011
UNIVERSITY EXAMINATIONS: 2010/2011
SECOND YEAR STAGE EXAMINATION FOR THE DEGREE OF BACHELOR
OF SCIENCE IN INFORMATION TECHNOLOGY
BIT 2207: OPERATIONS RESEARCH
DATE: AUGUST 2011 TIME: 2 HOURS
INSTRUCTIONS: Answer question ONE and any other TWO questions
Question One
a) A firm you work for manufactures two types of secondary storage devices; type A and B. For any
month it must produce at least 250 units of A and 100 units of type B. The maximum total
requirement of type A and B is 1,250 units and minimum total requirement is 500 units. Both types
are to be processed on machines M1 and M2. Total number of available machine hours is 3,000
hours for each machine. Processing times in hours for each of the devices on machines M1 and M2
are as follows:
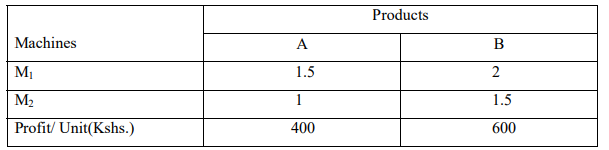
Formulate as a Linear Programming Problem. (6 Marks)
b) Explain in the context of the Transportation Problem:
i) Modified Distribution method
ii) Degeneracy test (4 Marks)
c) Discuss the costs associated with queuing systems and consequently the concept of optimum
servicing rate and optimum cost. (6 Marks)
d) State any four important distributions used for inter-arrival times and service times in queuing
models. (4 Marks)
e) Why is replacement of items required? Distinguish between individual replacement and group
replacement policies. (6 Marks)
f) Explain the following terms as used in Network analysis: (4 Marks)
i) Optimistic time
ii) Pessimistic time
iii) Most likely time
iv) Expected time
Question Two
a) i) Find an Initial basic Feasible solution and the corresponding total transportation costs, to
the following transportation problem using the North-west corner method:
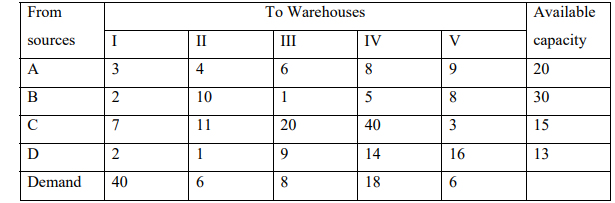
(8 Marks)
ii) Consequently find an optimal solution using the MODI method (6 Marks)
b) A Sales manager has to assign 4 salesmen to 4 territories. The possible profit for each salesman in
each territory is given below. Find the assignment that maximizes the profit.
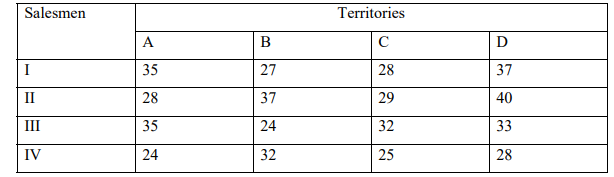
Question Three
a) Write short notes on the following:
(i) Necessity for inventory (2 Marks)
(ii) Types of inventory (2 Marks)
(iii) Inventory costs and their components (6 Marks)
b) An aircraft company uses Rivets at an approximate consumption rate of 2,500 kg per year. The
rivets cost K£30 per kg and the company personnel estimate that it costs K£130 to place an order.
The inventory carrying cost is 10 % per year.
(i) How frequently should orders for rivets be placed? (3 Marks)
(ii) What is the optimal quantity to be ordered? (3 Marks)
c) Illustrate with numerical examples the possible consequences if one solves an integer L.P problem
ignoring the ‘integer constraints’ and then rounding off the optimum non-integer values of the
optimum solution to integers. (4 Marks)
Question Four
a) Explain any four essential characteristics of Operations Research. (4 Marks)
b) A firm is thinking of replacing a particular machine whose cost price is K£15,300. The scrap price
of this machine is only K£ 300. The maintenance costs are found to be as follows:

Determine when the firm should get the machine replaced (8 Marks)
c) Find the sequence that minimizes the total elapsed time to complete the following jobs. Each job is
processed in the order AB
Find the total elapsed time and idle times for both machines. (8 Marks)
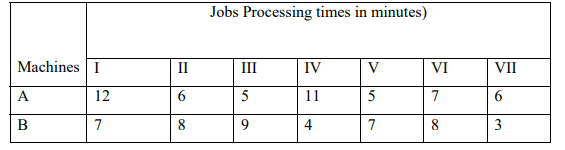
Question Five
a) A mother notes that when her teenage son uses the telephone, he takes no less than 10 minutes for a
call and sometimes as much as one hour. Twenty-minute calls are more frequent than calls of any
other duration. If the son’s phone call were an activity in a PERT network; what would (6 Marks)
i) Be the phone call’s expected duration?
ii) Be its variance?
b) You have been commissioned by the food manufacturer XYZ to carry out market research in a new
product development project prior to a test market launch. The table below lists required activities
and their durations in weeks.

i) Draw the product development network. (3 Marks)
ii) State the critical path and the project duration. (7 Marks)
iii) Prepare a table of the earliest start and completion times, the latest start and
completion times and the total and free floats. (4 Marks)
