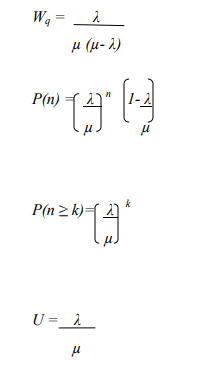UNIVERSITY EXAMINATIONS: 2012/2013
SECOND YEAR EXAMINATION FOR THE BACHELOR OF
SCIENCE IN INFORMATION TECHNOLOGY
BIT 2207 OPERATIONS RESEARCH
DATE: DECEMBER, 2012 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE
a) State any two Deterministic and any two Probabilistic techniques of Operations
Research you are familiar with. (4 Marks)
b) i. Justify the need to replace equipment by giving any four reasons(4 Marks)
ii. Distinguish between individual replacement and group replacement
policies (2 Marks)
c) Define the following terms as used in a Simplex problem.
i. Basic variable. (1 Mark)
ii. Non Basic variable. (1 Mark)
iii. Entering variable. (2 Marks)
iv. Leaving variable. (2 Marks)
d) Suggest the suitable model (whether iconic, analogue or symbolic) for the
following: (4 Marks)
i. Flow process chart in an organization.
ii. Histogram of the rainfall at a place.
iii. Economic order quantity formula
iv. An advertiser’s photo on a billboard.
e) State any two service disciplines as used in Queuing Theory. (2 Marks)
f) i. Determine an initial basic feasible solution to the following Transportation
problem using the Vogel’s Approximation method. (6 Marks)
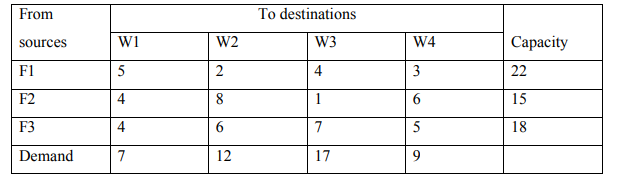
ii. Calculate the total Transportation cost for the schedule obtained in (i)
above (2 Marks)
QUESTION TWO
a) A company wishes to allocate its monthly budget of shs.1000,000 among three
advertising media; Television, Radio and Newspaper. The number of prospective
buyers reached by a single advertisement in the three media is 120,000, 28,000
and 40,000 respectively. The cost per advertisement is shs.20, 000, shs. 4,500 and
shs. 10,000 respectively. The company has decided that it will not release more
than 10, 20 and 10 advertisements in Television, Radio and Newspaper
respectively. The company wants to maximize the total audience coverage.
i. Formulate this as a Linear Programming Problem. (6 Marks)
ii. Write the Simplex tableau for finding the initial solution (6 Marks)
b) A marketing manager has 5 salesmen and 5 sales districts. Considering the
capabilities of the salesmen and nature of the districts, the marketing manager
estimates that sales per month (in thousands kshs. ‘000’) for each district would
be as follows:
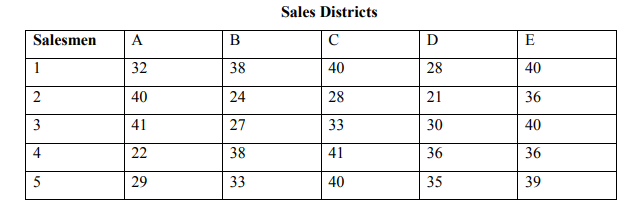
What is the maximum sale that may be expected if an optimum assignment is
made? (8 Marks)
QUESTION THREE
a) Workers come to a tool store room to receive special tools (required by them) for
accomplishing a particular project assigned to them. The average time between
two arrivals is 60 seconds and the arrivals are assumed to be in Poisson
distribution. The average service time (of the tool room attendant) is 40 seconds.
Assuming exponential service determine:
i. The average queue length (Lq) (3 Marks)
ii. Average number of workers in the system (Ls) (2 Marks)
iii. Mean waiting time of an arrival (2 Marks)
iv. The probability that there will be ten or more workers in the system at any time.
(3 Marks)
b) A book binder has one printing press, one book binding machine and manuscripts
of different books. The time required for performing printing and binding
operations for different books are shown below:
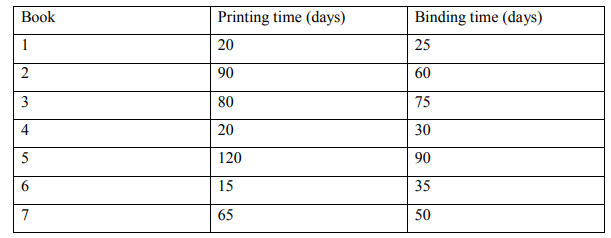
Determine the optimal sequence, total elapsed time and idle times for either
operation
(10 Marks)
QUESTION FOUR
a) Explain any three limitations of the use of Theory of Games. (6 Marks)
b) A project has the following activities and other related characteristics:
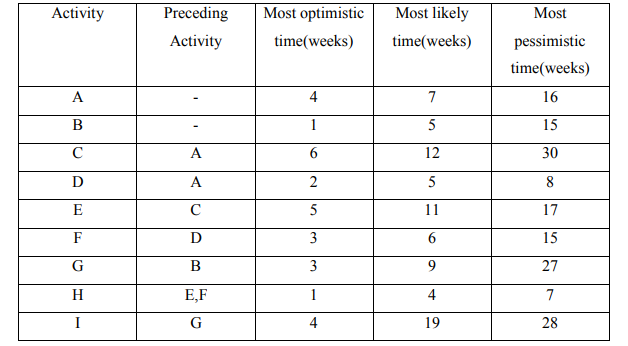
Required:
i. Determine the time estimates for each activity. (3 Marks)
(ii) Draw the PERT network diagram. (3 Marks)
ii. Determine the critical path and project completion time. (4 Marks)
iii. Find the probability that the project is completed in 36 weeks. (4 Marks)
QUESTION FIVE
Homa Tours Company operates some tourist flights around Game parks in Western
Kenya. At the moment they operate 3 small light aircrafts which are hired at the rate of
shs. 6, 000 per day, inclusive of all costs. At times a potential customer arrives only to
find all the three aircrafts booked for the day. The Company has a policy of paying out to
the customer sum of shs. 1, 000 as a consolation for each day, the customer waits before
he/ she is allocated an aircraft. Potential customers normally wait until they are allocated
an aircraft. Daily costs incurred by the Company to keep a single aircraft in the air are
shs. 2,000 per day. The following table shows the probability distribution for the number
of customers who seek services in a day.
Number of customers Probability
0 0.10
1 0.20
2 0.30
3 0.30
4 0.10
The three aircrafts are operated for 10 days in one season, unless customers are still
waiting at the end of the season.
a) Use the Monte Carlo Simulation technique and two digits random numbers
(see below) to simulate the above Business for 10 days-one season. (12 Marks)
b) How many customers were delayed at least for one day? (2 Marks)
c) What is the average queue length? (2 Marks)
d) Determine the total profit for the three aircrafts for the above Simulation Exercise
(4 Marks)
Random numbers
2 6 6 3 9 2 2 9 7 2 3 6 0 2 9 5 6 3 3 4
APPENDIX
Queuing Formulae
