
UNIVERSITY EXAMINATIONS: 2011/2012
YEAR II EXAMINATION FOR THE BACHELOR OF SCIENCE IN
INFORMATION TECHNOLOGY
BIT 2207 OPERATIONS RESEARCH
DATE: APRIL 2012 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One and Any other Two Questions
QUESTION ONE
a)Discuss any two models used in O.R with special emphasis on the assumptions made in each
model. (6 Marks)
b)Explain any two problems that one may encounter while using O.R tools. (4 Marks)
c)State the five basic requirements of the Linear programming model. (5 Marks)
d)Reduce the following Linear programming problem to its standard form, and consequently give
the initial basic solution using the Big M method. Minimize Z = 2×1+3×2+4×3
Subject to the constraints
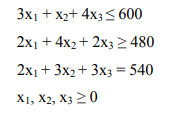
(6 Marks)
e)Explain how the theory of Replacement is used in replacement of items whose maintenance cost
varies with time and the value of money remains constant over time. (3 Marks)
f) Find the sequence that minimizes the total elapsed time and machine idle time required to
complete the following tasks. Each task is processed by the two machines in the order AB.

(6 Marks)
QUESTION TWO
a)Explain the following as used in Network Analysis: dangling, looping and false dependency.
(6 Marks)
b)A project has the following characteristics:

i. Draw the project network. (4 Marks)
ii. Find the critical path and the project completion time. (6 Marks)
iii. Prepare an activity schedule showing the Earliest Start time (EST), Earliest Completion
time (ECT), Latest Start time (LST) , the Latest Completion time (LCT),total float and
free float for each activity. (4 Marks)
QUESTION THREE
a)Write short notes on the assumptions made in single channel queuing theory. (5 Marks)
b)Describe a method for generating random numbers. Generate 10 random numbers using the
method described. (5 Marks)
c)The arrival and service times of customers have the following distributions. Simulate this
queuing system for 10 periods using the random numbers provided below, and calculate the
mean waiting time and the mean queue length.
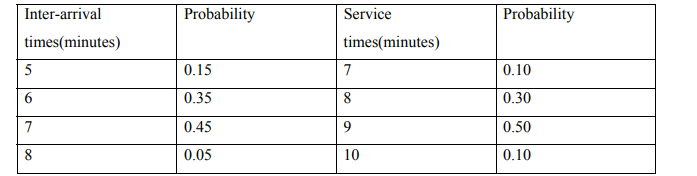
Random numbers for arrivals:36,60,82,14,,14,62,62,10,55,14.
Random numbers for service:34,35,31,62,48,73,88,70,19,40. (10 Marks)
QUESTION FOUR
a)Five employees of a firm are to be assigned to five jobs, which can be done by any of them. The
amount of time in hours per day by each employee to do a given job is as given below:
Job
Employee
A B C D E
1 7 9 3 3 2
2 6 1 6 6 5
3 3 4 9 10 7
4 1 5 2 2 4
5 6 6 9 4 2
i. Determine the assignment schedule that minimizes the total time taken to turn out all the
jobs. (10 Marks)
ii. The five workers get different wages per hour, K£5 per hour for workers A, B and C, while
workers D and E get K£3 per hour. Determine the assignment schedule that minimizes the
total cost of turning out the five jobs. (10 Marks)
QUESTION FIVE
a)Explain any three advantages and three disadvantages of holding inventory. (6 Marks)
b)List three methods of obtaining an initial basic feasible solution for a Transportation problem.
Which is the best among them and why? (4 Marks)
c)A drug manufacturing concern has ten medical representatives working in three sales areas. The
profitability for each representative in the sales areas is as follows:
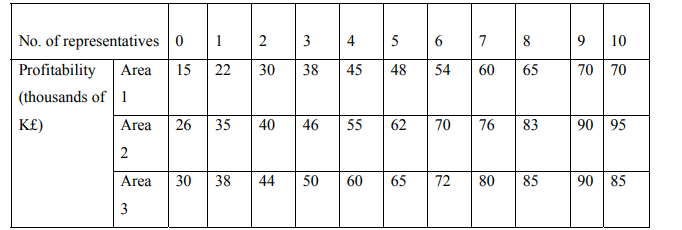
i. Determine the optimum allocation of medical representatives in order to maximize the
profits.(Hint: A dynamic programming problem) (10 Marks)
