 UNIVERSITY EXAMINATIONS: 2014/2015
UNIVERSITY EXAMINATIONS: 2014/2015
ORDINARY EXAMINATION FOR THE BACHELOR OF SCIENCE
IN INFORMATION TECHNOLOGY
BIT 2201 SIMULATION AND MODELING
DATE: APRIL, 2015 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE: 30 MARKS (COMPULSORY)
a) It is not always possible to experiment and study with real systems hence the need for
modeling. Discuss three reasons why that is so. (3 marks)
b) Discuss five applications of simulation and modeling in real life (5 marks)
c) Using the mid- square method obtain the random variables using Z0= 1009 until the
cycle degenerates to zero. (7 marks)
d) Discuss any five desirable features of a good simulation software (5 marks)
e) Using the banking systems as an example describe the components of a discreteevent system. (10 marks)
QUESTION TWO: 20 MARKS
a) Every system exists with an environment. Activities in the system’s environment
cause changes in the state of the system. These activities are classified into two
categories: Endogenous and Exogenous. Differentiate between the two. (2 marks)
b) Discuss four reasons why it is necessary to use animation during the process of
modeling and simulation. (4 marks)
c) State and briefly explain four properties of a good arithmetic random number
generator. (4 marks)
d) Describe five common statistics included in the output report of a simulation
programming system. (10 marks)
QUESTION THREE: 20 MARKS
a) There are two fundamental types of animation; concurrent and post-processed
Differentiate between the two types of animation. (2 marks)
b) Describe the following terms giving examples from the communication systems.
(5 marks)
i) State of a System
ii) State Variables
iii) Entity
iv) Attribute
v) Activity
c) Discuss four drawbacks simulation and modeling. (4 marks)
d) Using the Linear Congruential Generator (LCG) with a=5, m=16, c=3 and seed Z0 = 7
to generate the first FIVE random variates on [0,1]. (5 marks)
e) Discuss the two short comings of the mid-square method as a random number
generator. (4 marks)
QUESTION FOUR: 20 MARKS
a) Define the terms verification and validation in the context of modeling. (4 marks)
b) Not all simulation and modeling exercises are a success. Discuss five common pitfalls
to successful simulation. (5 marks)
c) Consider a single server queuing system in the bank. The system starts at time t=0.
The arrival time of customers is: 0.4, 1.6, 2.1, 3.8, 4.0, 5.6, 5.8, and 7.2. The
departure times are: 2.4, 3.1, 3.3, 4.9, and 8.6. Time is in minutes. The first in first out
queuing discipline is followed. Simulate this system for six clients and estimate:
i) The expected average delay in the queue (3 marks)
ii) The expected average number of clients in the in the at any time t
(6 marks)
iii) The expected utilization of server. (2 marks)
QUESTION FIVE: 20 MARKS
a) Differentiate between the following types of models (6 marks)
i) Deterministic Vs Stochastic Models
ii) Discrete Models Vs Continuous Models
b) Discuss any five advantages of simulation (5 marks)
c) The table below shows the probability distribution of a container arrivals per day at
Mombasa port.
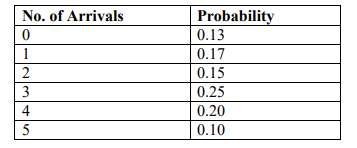
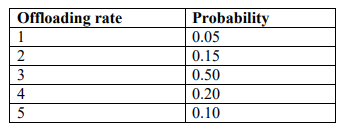
The offloading rate per day follows the probability distribution given below. NB:
Offloading is done on FCFS basis.
Offloading rate Probability
Suppose the following are the random numbers of arrivals and random numbers of
unloading.
Arrival Random No. 52, 06, 50, 88, 53, 30, 10, 47, 99, 37, 66, 91, 35, 32, 00
Offload Random No. 37, 63, 28, 02, 74, 35, 24, 03, 29, 60, 74, 85 90, 73, 59
Required: simulate a fifteen day analysis and determine:
i) The average number of container delayed (3 marks)
ii) The average number of arrivals per day (3 marks)
iii) The average number of containers offloaded each day (3 marks)
