 UNIVERSITY EXAMINATIONS: 2012/2013
UNIVERSITY EXAMINATIONS: 2012/2013
FIRST YEAR EXAMINATION FOR THE BACHELOR OF SCIENCE
IN INFORMATION TECHNOLOGY
BIT 1301 PROBABILITY AND STATISTICS
DATE: AUGUST, 2013 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO Questions
QUESTION ONE
a) Briefly define the following terms as used in probability and statistics.
i) Sample space
ii) Frequency distribution
iii) Arithmetic mean
iv) Kurtosis
v) Correlation
iv) Mutually exclusive event (6 Marks)
b) Thirty army inductees were given a blood test to determine their blood type. The
data set is as follows:
A B B AB O A
O O B AB B O
B B O A O B
A O O O AB B
AB A O B A AB
Construct a frequency distribution for the data. (2 Marks)
c) i) Using a clearly labeled diagram, show the position of the mean, mode and
median of a positively skewed distribution. (2 Marks)
ii) Given the data set 33, 35, 37, 37, 39, 39, 41, 41, 41, 42, 44, calculate the
mean, median and standard deviation. Hence calculate the first Pearson’s
coefficient of skewness. Comment on the distribution of the data. (7 Marks)
100 students pursuing a course in IT were examined and their results were
summarized as shown in the table below:
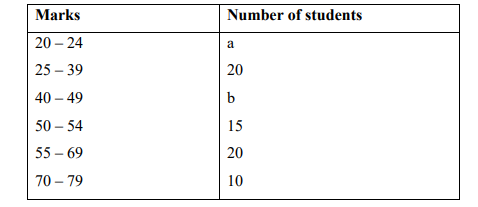
Given that the median mark is 47.5. Determine the values of a and b.
(5 Marks)
d) Check the following data set for outliers. 5, 6, 12, 13, 15, 18, 22, 50
(6 Marks)
e) In a hospital unit, there are eight nurses and five physicians. Seven nurses and three
physicians are females. If a staff is selected, find the probability that the subject is a
nurse or a female. (2 Marks)
QUESTION TWO
i) a) Two discs are drawn without replacement from a box containing three red and
four white discs. If X is the random variable “the number of white discs
drawn”, find:
i)
E x (6 Marks)
ii)
2 E x (2 Marks)
i)
Var x (2 Marks)
ii)

Calculate
i) The mean of the data
ii) The mode
iii) The median (8 Marks)
QUESTION THREE
a) The data obtained in a study of age and systolic blood pressure of six randomly
selected subjects is shown below:
Subject A B C D E F
Age(x) 43 48 56 61 67 70
Pressure(y) 128 120 135 143 141 152
i) Compute the value of the correlation coefficient and comment.
ii) Find the equation of the regression line of y on x.
iii) What is the blood pressure of a 50 year old person? (10 marks)
b) Differentiate between a discrete and a continuous random variable. (2 Marks)
c) A teacher gives a 20 point test to 10 students. The scores are18, 15, 12, 6, 8, 2, 3,
5, 20, 10. Find
i) percentile rank of a score of 12.
ii) the value corresponding to the 25th percentile
iii)the value that corresponds to the 60th percentile. (8Marks)
QUESTION FOUR
The masses in grams of 50 small fruits are shown in the following table,
Mass grams Number of Fruits
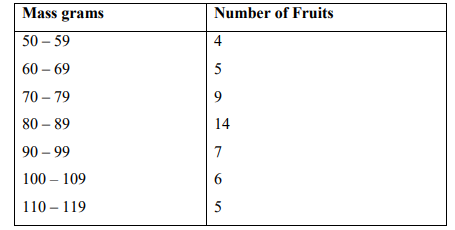
Calculate the:
a) Mean (2 Marks)
b) Mode (2 Marks)
c) Median (3 Marks)
d) Standard deviation (4 Marks)
e) Interquartile range (3 Marks)
f) First Pearson’s coefficient of skewness (2 Marks)
g) Percentile coefficient of Kurtosis and comment. (4 Marks)
QUESTION FIVE
a) A group of computer science students sat probability and statistics and programming
papers in the April 2013 examination. The marks obtained by the candidates were as
follows.
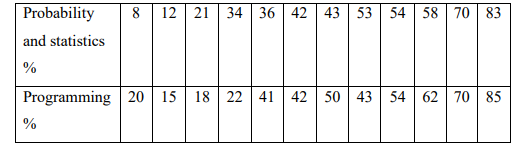
i) Determine the rank correlation coefficient and comment on its value.
(6 Marks)
b) A recent survey asked 100 people if they thought women in the armed forces should
be permitted to participate in combat. The result of the survey are shown in the table:

Find these probabilities:
i) The respondent answered “Yes” given that the respondent was a female
ii) The respondent was a male, given that the respondent answered “No”
(6 marks)
c) In a large restaurant, the following probability distribution was obtained for the
number of items a person ordered for a large pizza.

Find the mean of the distribution. (2 Marks)
d) An exclusive college desires to accept only the top 10% of all graduating seniors
based on the results of a national placement test. This test has a mean of 500 and a
standard deviation of 100. Find the cutoff score for the exam. Assume the variable is
normally distributed. (6 marks)
