 UNIVERSITY EXAMINATIONS: 2012/2013
UNIVERSITY EXAMINATIONS: 2012/2013
FIRST YEAR EXAMINATION FOR THE BACHELOR OF SCIENCE
IN INFORMATION TECHNOLOGY
BIT 1301 PROBABILITY AND STATISTICS
DATE: DECEMBER, 2012 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE
Twenty five army inductees were given a blood test to determine their blood type. The
data set is as follows:
A B B AB O
O O B AB B
B B O A O
A O O O AB
AB A O B A
a) Construct a frequency distribution for the data. (2 Marks)
b) Check the following data set for outliers. 5, 6, 12, 13, 15, 18, 22, 50 (6 Marks)
c) A random sample of the life expectancy of residents for 25 countries in Africa
was selected and the following frequency distribution was obtained.
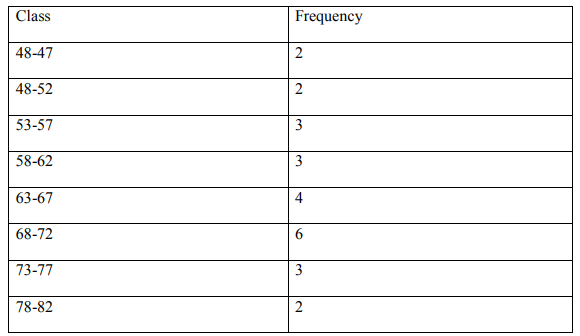
Calculate:
i) The mean
ii) The mode
iii) The median
iv) The standard deviation
v) The 90th and 10th percentile
vi) Coefficient of Skewness and comment
(14 Marks)
d) Three cards are drawn from an ordinary deck and not replaced. Find the
probability of the following.
i) Getting three jacks
ii) Getting an ace, a king and a queen in order
iii) Getting a club, a spade and a heart in order.
iv) Getting three clubs.
(8 Marks)
QUESTION TWO
a) A student scored 65 on a calculus test that had a mean of 50 and a standard
deviation of 10, she scored 30 on a history test with a mean of 25 and a standard
deviation of 5. Compare her relative positions on the two tests. (5 Marks)
b) An insurance company researcher conducted a survey on the number of car thefts
in Nairobi for a period of 30 days last month. The raw data are shown below:
52 62 51 50 69 58 77 66 53 57
75 56 55 67 73 79 59 68 65 72
57 51 63 69 75 65 53 78 66 55
Construct a stem and leaf plot by using classes 50-54, 55-59, 60-64, 65-69, 70-74,
and 75-79. (6 Marks)
c) A recent survey asked 100 people if they thought women in the armed forces
should be permitted to participate in combat. The result of the survey are shown
in the table:
Gender Yes No
Male 32 18
Female 8 42
Find these probabilities:
i) The respondent answered “Yes” given that the respondent was a female
ii) The respondent was a male, given that the respondent answered “No”
(6 Marks)
d) In a large restaurant, the following probability distribution was obtained for the
number of items a person ordered for a large pizza.
Number of
items X
0 1 2 3 4
Probability
P(X)
0.3 0.4 0.2 0.06 0.04
Find the mean of the distribution.
(3 Marks)
QUESTION THREE
a) On new year’s eve, the probability of a person driving while intoxicated is 0.32,
the probability of having a driving accident is 0.09, and the probability of a person
having a driving accident while intoxicated is 0.06. What is the probability of a
person driving while intoxicated or having a driving accident. (3 Marks)
b) Five balls numbered 0, 2, 4, 6 and 8 are placed in a bag. After the balls are mixed,
one is selected, it’s number is noted and then it is replaced. If this experiment is
repeated many times, find the variance and standard deviation of the numbers on
the balls. (6 Marks)
c) The data obtained in a study of age and systolic blood pressure of six randomly
selected subjects is shown below:
Subject A B C D E F
Age(x) 43 48 56 61 67 70
Pressure(y) 128 120 135 143 141 152
i) Compute the value of the correlation coefficient and
comment.
ii) Find the equation of the regression line of y on x.
iii) What is the blood pressure of a 50 year old person.
(11 Marks)
QUESTION FOUR
a) An exclusive college desires to accept only the top 10% of all graduating seniors
based on the results of a national placement test. This test has a mean of 500 and a
standard deviation of 100. Find the cutoff score for the exam. Assume the variable
is normally distributed. (6 Marks)
b) The president of a large university wishes to estimate the average age of the
students presently enrolled. From past studies, the standard deviation is known to
be 2 years. A sample of 50 students is selected and the mean is found to be 23.2
years. Find the 95% confidence interval of the population mean. (6 Marks)
c) A teacher gives a 20 point test to 10 students. The scores are18,15, 12, 6, 8, 2, 3,
5, 20, 10.
Find
i) Percentile rank of a score of 12.
ii) The value corresponding to the 25th percentile
iii) The value that corresponds to the 60th percentile.
(8 Marks)
QUESTION FIVE
a) A marketing specialist wishes to see whether there’s a difference in the average
time a customer has to wait in a check out line in three large self service
departmental stores. The time in minutes is shown below:
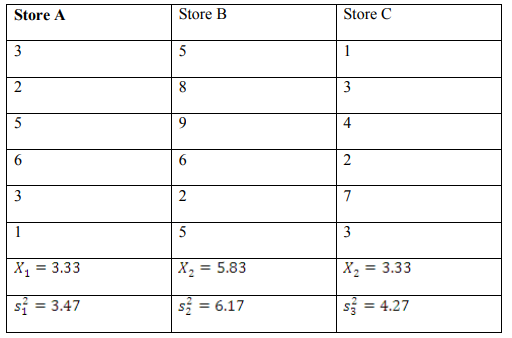
At , is there a significant difference in the mean waiting times of
customers for each store? (8 Marks)
b) In a hospital unit, there are eight nurses and five physicians. Seven nurses and
three physicians are females. If a staff is selected, find the probability that the
subject is a nurse or a female. (2 Marks)
c) Given the data below:
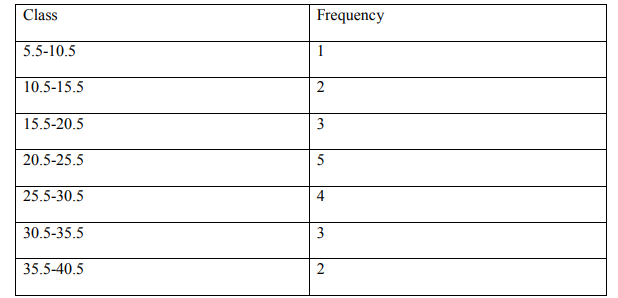
Caalculte
i) The mean of the data
ii) The mode
iii) The median
iv) The standard deviation
(10 Marks)
