
UNIVERSITY EXAMINATIONS: 2021/2022
ORDINARY EXAMINATION FOR BACHELOR OF SCIENCE
INFORMATION TECHNOLOGY, BSc. APPLIED COMPUTING, BSD,
BISF, BBIT
BIT 1301/ BUSS 202/ BSD 1203/ BISF 1202/ BAC 1202: PROBABILITY
AND STATISTICS
(EVENING/ DISTANCE LEARNING)
DATE: DECEMBER, 2021 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One and any Other Two Questions
QUESTION ONE
(a)The arithmetic mean of a distribution is 5.The second and the third moments
of the distribution about the mean are 20 and 140 respective. Find the third
moment of the distribution about10 [8Marks]
(b)A certain distribution has karl pearsons coefficient of skewness 0 ⋅ 4,
standard deviation 10 and mean 40.5.Find the mode and the median of the
distribution . [8Marks]
(c)If ?,? and ? are mutually independent events ,show that ? and ? ∪ ? ∪ ?
are independent. [4Marks]
QUESTION TWO
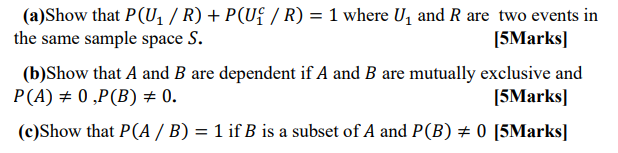
QUESTION THREE
(a) A fair coin is tossed 8 times.
(i)What is the probability that the eighth toss results in a head given that
preceeding 7 tosses were heads? [5Marks]
(ii) What is the probability of getting eight heads or eight tails if the fair coin is
tossed 8 times? [5Marks]
(b)A student is taking multiple choice exam in which each question has four
possible answers ,exactly one which is correct.If the student knows the answer
he(she)selects one answer at random from the four possible answers.Suppose
that the student knows the answers to 55% of the questions.
(i)What is the probability that on a given question the student gets the correct
answer? [2Marks]
(ii)If the student gets the correct answer to a question what is the probability
that he or she knows the answer? [3Marks]
QUESTION FOUR
(a)Determine the constant ? so that the function given below is a probability
distribution of the random variable ? .

[4Marks]
(c)Bank tellers in a certain bank make errors in entering figures in their ledgers
at a rate of 0.8 errors per page of entry..What is the probability that in five
pages there will be three or more or
errors? [3Marks]
(d)Use the normal approximation to the binomial to calculate the probability of
getting more than 39 defectives in a random sample of 400 taken from a
population which is 8% defective. [4Marks]
