
UNIVERSITY EXAMINATIONS: 2014/2015
ORDINARY EXAMINATION FOR THE BACHELOR OF SCIENCE
IN INFORMATION TECHNOLOGY
BIT 1206 DISCRETE MATHEMATICS
DATE: DECEMBER, 2014 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE (30 MARKS)
a) i) Define the term Boolean algebra (2 Marks)
ii) Use Boolean laws to show that

d) How many committees of five people can be chosen from twelve men and twenty
women? If exactly three women must be chosen on each committee.
(4 Marks)
e) Write the following relations as set of ordered pairs
i). R1
is from A ={2, 5, 7, 8,} into B ={1, 3, 4,10,16} defined by aR1
b if
and only if a divides b.

QUESTION TWO (20 MARKS)
a) Define the following terms
i). Poset (2 Marks)
ii). Lattice (2 Marks)
b) Draw a Hasse diagram for the following set under the divisibility relation
{1,2,3,4,6,9,12,36,72,} .Showing all the steps. (6
Marks)
i). Find the maximal and minimal elements (2 Marks)
ii). Is there greatest and least elements? (2 Marks)
iii).Find all upper bounds and lower bounds of the set (6,9,12)
(2 Marks)
iv). Find least upper bounds and greatest lower bounds of (6,9,12)
(2 Marks)
v). Is the Poset a lattice? Give reasons for your answer. (2 Marks)
QUESTION THREE (20 MARKS)
a) i). Construct the truth table for the Boolean expression
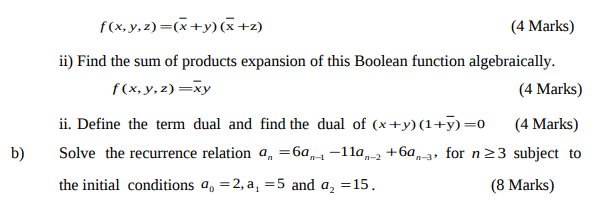
QUESTION FOUR (20 MARKS)
a) Draw the multigraph, G corresponding to the following adjacency matrix A.

QUESTION FIVE (20 MARKS)


