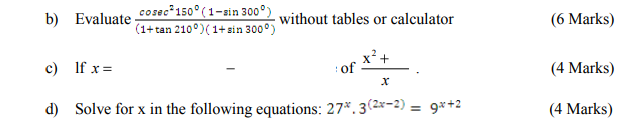UNIVERSITY EXAMINATIONS: 2012/2013
FIRST YEAR EXAMINATION FOR THE BACHELOR OF SCIENCE
IN INFORMATION TECHNOLOGY
BIT 1110 MATHEMATICS FOR SCIENCE
DATE: DECEMBER, 2012 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE
a) A basket holds 3 lemons and 7 tangerines. Njeri picked two fruits at random. What
is the probability that:
i) both were tangerines?
ii) There was one lemon and there was one tangerine?
iii) There was at least one tangerine?
(6 Marks)
b) If and A is obtuse, find the value of (4 Marks)
c) The third and fifth terms of an arithmetic progression are 10 and -10 respectively.
d) Determine
i) The first term and the common difference
ii) The sum of the first 15 terms.
(6 Marks)
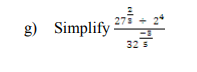
QUESTION TWO
a) The table below shoes the marks scored by 100 Form two students in a mathematics
test.
i) state the modal class
ii) calculate the mean mark for the student
iii) calculate the standard deviation.
(7 Marks)
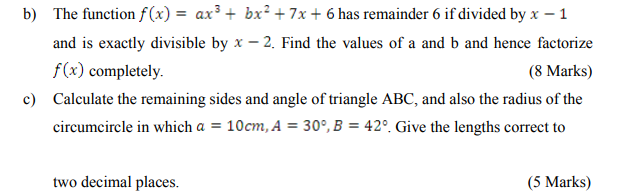
QUESTION THREE
a) Two lorries A and B ferry goods between two towns which are 33120km apart.
Lorry A travelled at 5km/h faster than lorry B and lorry B took 4 hrs more than
lorry A to cover the distance. Calculate the speed of lorry B. (8 Marks)
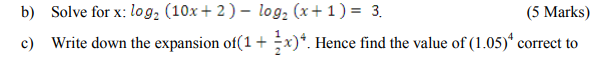
d) In how many ways can the letters in the word MISSISSIPPI be arranged? (2 Marks)
QUESTION FOUR
b) At the beginning of every year, a lady deposited Ksh 10 000 in a financial
institution which paid compound interest at the rate of 20% p.a. She stopped further
deposits after three years. The money remained invested in the institution for a
further eight years.
i) How much money did she have at the end of the first three years?
(5 Marks)
ii) How much interest did the money generate in the entire period (5 Marks)
c) Solve the equation:
2 1 2 5 3 x x
(4 Marks)
QUESTION FIVE
a) In a geometric progression, the third term is 81 and the sixth term is 3. Determine
the first term, the common ratio and the sum to infinity of the series. (6 Marks)
