 UNIVERSITY EXAMINATIONS: 2010/2011
UNIVERSITY EXAMINATIONS: 2010/2011
FIRST YEAR STAGE EXAMINATION FOR THE DEGREE OF BACHELOR
OF SCIENCE IN INFORMATION TECHNOLOGY
BIT 1101: LINEAR ALGEBRA
DATE: AUGUST 2011 TIME: 2 HOURS
INSTRUCTIONS: Answer question ONE and any other TWO questions
Question One
a) Define the following terms as used in Algebra: (9 Marks)
i) Eet
ii) Product set
iii) Tautology
iv) Power set
v) Proposition
vi) Conjuction
vii) Contradiction
viii) Argument
ix) Fallacy
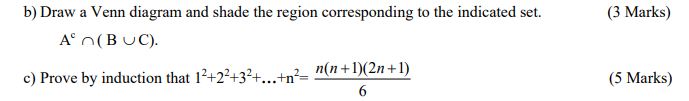
d) In a survey of 60 people, it was found that 25 read Newsweek, 26 read Time and 23 read fortune.
Also 11read both Newsweek and Time, 9 read Newsweek and Fortune, 8 read both Time and
Fortune, and 3 read all three magazines. Find the number of people who read: (8 Marks)
i) Only Newsweek
ii) Only Time
iii) Only Fortune
iv) Newsweek and Time, but not fortune
v) Only one of the magazines
vi) None of the magazines.
e) Show that “p implies q and q implies p” is logically equivalent to the bicondittional “p if and only
if q”. (5 Marks)
Question Two

Question Three
a) Express the specification “The automated reply cannot be sent when the file system is full” using
logical connectives. (4 Marks)
b) Determine whether these system specifications are consistent:
“The diagnostic message is stored in the buffer or it is retransmitted”
“The diagnostic message is not stored in the buffer”
“If the diagnostic message is stored in the buffer, then it is retransmitted”. (5 Marks)
c) Use predicates and quantifiers to express the system specifications “ Every mail message larger
than one megabyte will be compressed” and “ if a user is active, at least one network link will be
available” (3 Marks)
d) Consider these statements of which the first three are premises and the fourth is a valid conclusion.
“All hummingbirds are richly covered”
“No large birds live on honey”
“Birds that do not live on honey are dull in color”
“Hummingbirds are small”.
Let P(x), Q(x), R(x) and S(x) be the statements “x is a hummingbird”,”x is large”, “x lives on
honey”, “x is richly colored”, respectively. Assuming that the domain consists of all birds, express
the statements in the argument using the quantifiers P(x), Q(x), R(x) and S(x). (8Marks)
Question Four
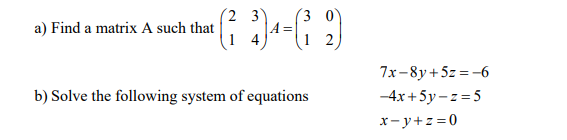
Using
i) Substitution and elimination method (5 Marks)
ii) Inverse method (9 Marks)
Question Five
a) How many different six figure phone numbers are possible if the digits 0 to 9 are allowed except
that the first digit must be 7,8 or 9. (2 Marks)

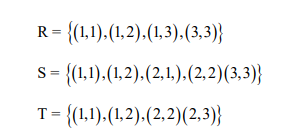
i) Reflexive
ii) Symmetric
iii) Transitive
iv) Antisymmetric
e) Give reasons for your answer
