
UNIVERSITY EXAMINATIONS: 2014/2015
ORDINARY EXAMINATION FOR THE BACHELOR OF BUSINESS
INFORMATION TECHNOLOGY
BCU 102 FOUNDATIONS OF MATHEMATICS – DISTANCE
LEARNING
DATE: DECEMBER, 2014 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE (30 MARKS)
a) Find the converse, inverse and contra positive of the implication “if today is Sunday,
then I will go to church ” (3 marks)
b) Construct the truth table for the following statement formula:
![]()
c) Test the validity of this argument “if Peter solved seven problems correctly, then Peter obtained the grade A. therefore Peter solved seven problems correctly. (6 marks)
d) In a recent survey of 400 students in a college,100 were listed as studying typing,150
were listed as studying accountancy and 75 were registered for both courses.
i. Represent the above information in a Venn diagram.
ii. Determine the number of students registered for typing only.
iii. Determine the number of students registered for accountancy only.
Determine of students in the college who were not registered for either typing or
accountancy
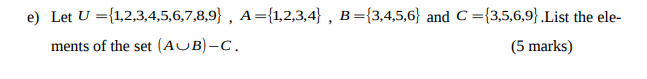
QUESTION TWO (20 MARKS)
a) Define the term proposition. (2 marks)
b) Determine whether the following argument form is valid.
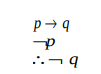
c) Write the negative of each of the following statements
i) 2 is positive
ii) Today is Sunday
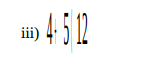
d) Show that formula A : ( p → q) ∧ ( q → r) is logically equivalent to form B : p →(q ∧r)
(6 marks)
QUESTION THREE (20 MARKS)
a) Let a, b and c be integers, then prove that for any integer a, a ×0 = 0 (4 marks)
b) Use direct proof to show that product of two odd integers is an odd integer.
(6 marks)
c) Show by truth table for each of the following statement formula is a tautology.
¬ p → ( p → q) (5 marks)
d) Prove or disapprove that
( p → q) ∨ (¬ p → q) and q are logically equivalent. (5 marks)
QUESTION FOUR (20MARKS)
a) What is the truth value of the quantification∀x p(x) ? The domain of the discourse
is the set of all positive integers.
i. p( x) : ( x +1) ( x + 2) is an even integer
ii. p( x) : x + 1〉 x
iii. p( x) : x + 2 〉 5
iv. ( ) : x 2 3
2
p x + = (4 marks)
b) Let U ={1, 2, 3, 4, 5, 6 , 7} , A ={1, 3, 4, 6} and B ={2, 4, 5} be sets, where U acts as the
universal set. Determine the following.
i. ( )
/
A∪B
ii. ( A∩B)
iii. A − B
iv. B −C (4 marks)
c) Give a direct proof to show that if x and y are even integers, then x + y is an
even integer. (5
marks)
d) Use indirect proof to prove the following. Let n be an integer. If 3
2
n + is odd then n
is even. (7marks)
QUESTION FIVE (20MARKS)

