
MAASAI MARA UNIVERSITY
REGULAR UNIVERSITY EXAMINATIONS
2015/2016 ACADEMIC YEAR
FIRST YEAR SECOND SEMESTER
SCHOOL OF: BUSINESS AND ECONOMICS
BACHELOR OF: BUSINESS MANAGEMENT/ EDUCATION
COURSE CODE: BBM 105
COURSE TITLE: BUSINESS MATHEMATICS I
DATE: 4TH MAY 2016 TIME:8.30-10.30 AM
INSTRUCTIONS TO CANDIDATES
1. Answer Question ONE and any other THREE questions
2. Question ONE carries 25 marks
3. Involvement in exam cheating will lead to discontinuation
QUESTION ONE (25 MKS)
a) Differentiate the following terms giving examples:
i) Universal set and Complement of asset(2mks)
ii) Simple Interest and Compound Interest(2mks)
iii) Average rate of change and Instantaneous Rate of Change(2mks)
iv) Amortization and Sinking fund(2mks)
v) Linear equation and Quadratic equation(2mks)
b) Nyamongo Limited has the following demand functions for product N.
Demand function; p=300-q2
Where p=price per unit of product N.
q=quantity produced and sold
Determine the:
i) Quantity that will maximize revenue (2mks)
ii) Price that will maximize revenue (2mks)
iii) Maximum total revenue (1mk)
c) In the first week of September 2015 Mwenje a trader sold one shirt and three pairs of rubber shoes, making total sells of kshs.1500. in the second week, he sold four shirts and one pair of rubber shoes making total sells of Kshs.2,700.
Required
i) Formulate simultaneous equations from the above information (2mks)
ii) Determine the selling price of each item (2mks)
d) Nduta has a plan to buy a car after three years. The car is expected to cost kshs.220,000. To achieve this plan she deposited in a bank Kshs.80,000 to the beginning of the first year and Kshs.40,000 at the beginning of the second year. The bank pays compound interest at the rate of 10% per annum. Calculate the amount which she should deposit at the beginning of the third year in order to purchase the car. (6mks)
QUESTION TWO (15MKS)
a) A news agency limited deals with the distribution of three types of magazines. Newline, informer and update. A market survey of 100 people revealed; 48 read Newsline, 18 read informer, 26 read update, 8 read newsline and update, 8 read newsline and Informer, 3 read update and Informer and 3 read the three magazines.
Required
i) Represent the above information using a venn diagram (4mks)
ii) How many of the people surveyed:-
a) Read the Newsline but did not read informer (2mks)
b) Read update and informer but did not read the Newsline (2mks)
c) Read none of the magazines. (2mks)
b) A company produces three products X, Y and Z which are processed through three departments namely PQ and R. The table below shows the labour hours required to produce one unit of each product in each of the departments.
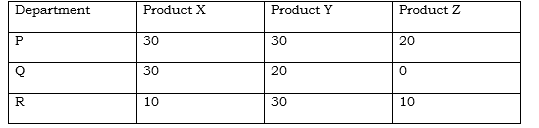
The monthly labour hour capacity for the three departments are 13000,8500 and 6000 hours fro department P Q and R respectively.
Required
a) Model the above problem as a system of simultaneous equations. (2mks)
b) Solve the model above to determine the optimal combination of the products that could be produced each month. (3mks)
QUESTION THREE (15MKS)
A firm intends to borrow ksh.1,000,000 to be invested in either project 1 or project 2. The annual interest payable to 15%. The following are the expected cash flows for the two projects.
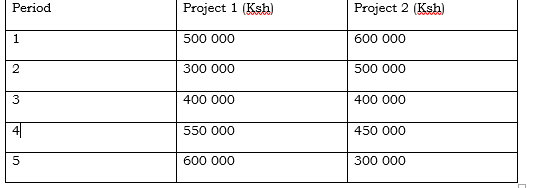
Required
i) Calculate the NPV of each project. (3mks)
ii) Calculate the pay back period of each project. (3mks)
iii) Advice the management of the firm on the project to invest based on 1 and 2 above (2mks)
c) A firm conducted a survey on the demand of one of its products and established the demand function to be
d) Q=500p+12,500
Where q is the number of units demand at price p.
The estimated fixed cost to produce one unit of the product was ksh.6,000 while the variable cost was ksh.5 per unit. Calculate:
i) Quantity that would be produced to maximize profits. (3mks)
ii) Selling price per unit that would maximize profits. (4mks).
QUESTION FOUR (15 MKS)
a) Chebet is not familiar with time value of money. She has asked you to help her to calculate her net worth in the future if she invested sh.50,000 today for a period of 3 years if rate is 10%
i) Interest is compounded annually (2mks)
ii) Interest is compounded monthly. (2mks)
b) Mugo and Mugo Associates have recently started giving business advice to their clients. Acting as consultants, they have estimated the demand curve for their clients as AD=200-8Q, where AR is average revenue in millions of shillings and Q is the output in units. Investigations into the firm’s cost profile shows that marginal cost (MC) is given by MC=Q2-28Q-211. Further investigations have shown that the firm’s cost when not producing output is sh.10 million.
Required
i) The equation of total cost (3mks)
ii) The equation of total revenue (2mks)
iii) An expression for profit (3mks)
iv) The level of output that maximizes profit (3mks)
QUESTION FIVE (15 MKS)
a) Given that A=(a,b,g,h) B=(a,c,g,I,k) C=(c,g,h,k) determine the composition of the following relations.
i) AUC (2MKS)
ii) AnB (2mks)
iii) AnBnC (2mks)
iv) (AUB)n(AUC) (2mks)
b) Outline three used of functions in business (3mks)
c) Nyamongo Limited has the following demand functions for product N.
Demand function; p=300-q2
Where P=price unit of product N.
q=quantity produced and sold
Determine the:
i) Quantity that will maximize revenue (2mks)
ii) Price that will maximize revenue (1mks)
iii) Maximum total revenue (1mk)
